In this chapter we see how the Haskell language features we introduced in previous chapters (from function application rules based on Lambda CalculusA model of computation based on mathematical functions proposed by Alonzo Church in the 1930s. to Typeclasses) lead to highly flexible and refactorable code and powerful abstractions.

Learning Outcomes

Refactoring Cheatsheet

The following equivalences make many refactorings possible in Haskell:

Eta Conversion

Exactly as per Lambda CalculusA model of computation based on mathematical functions proposed by Alonzo Church in the 1930s. :

f x ≡ g x
f   ≡ g

Operator Sectioning

Remember haskell binary operators are just infix curried functionsFunctions that take multiple arguments one at a time and return a series of functions. of two parameters and that putting brackets around them makes them prefix instead of infix.

x + y ≡ (+) x y
      ≡ ((+) x) y  -- making function application precedence explicit
      ≡ (x+) y     -- binary operators can also be partially applied

Such operator sectioningThe process of partially applying an infix operator in Haskell by specifying one of its arguments. For example, (+1) is a section of the addition operator with 1 as the second argument. allows us to get the right-most parameter of the function on it’s own at the right-hand side of the body expression such that we can apply eta conversionSubstituting functions that simply apply another expression to their argument with the expression in their body. This is a technique in Haskell and Lambda Calculus where a function f x is simplified to f, removing the explicit mention of the parameter when it is not needed. , thus:

f x = 1 + x
f x = (1+) x
f = (1+)             -- eta conversion

Compose

Has its own operator in haskell (.), inspired by the mathematical function composition symbol ∘:

 (f ∘ g) (x) ≡ f (g(x)) -- math notation
 (f . g) x ≡ f (g x)    -- Haskell

Again, this gives us another way to get the right-most parameter on its own outside the body expression:

f x = sqrt (1 / x)
f x = sqrt ((1/) x)     -- operator section
f x = (sqrt . (1/)) x   -- by the definition of composition
f = sqrt . (1/)         -- eta conversion

Point-Free Code

We have discussed point-free and tacit coding style earlier in these notes. In particular, eta-conversion works in Haskell the same as in lambda calculusA model of computation based on mathematical functions proposed by Alonzo Church in the 1930s. and for curried JavaScript functions. It is easy to do and usually declutters code of unnecessary arguments, e.g.:

lessThan :: (Ord a) => a -> [a] -> [a]
lessThan n aList = filter (<n) aList

The following is more concise, and once you are used to reading haskell type definitions, just as self evident:

lessThan :: (Ord a) => a -> [a] -> [a]
lessThan n = filter (<n)

But the above still has an argument (a point), n. Can we go further?

It is possible to be more aggressive in refactoring code to achieve point-free styleA way of defining functions without mentioning their arguments. by using the compose operatorRepresented as (.) in Haskell, it allows the composition of two functions, where the output of the second function is passed as the input to the first function. (.):

(.) :: (b -> c) -> (a -> b) -> a -> c
(f . g) x = f (g x)

To see how to use (.) in lessThan we need to refactor it to look like the right-hand side of the definition above, i.e. f (g x). For lessThan, this takes a couple of steps, because the order we pass arguments to (<) matters. Partially applying infix operators like (<n) is called operator sectioningThe process of partially applying an infix operator in Haskell by specifying one of its arguments. For example, (+1) is a section of the addition operator with 1 as the second argument. . Placing n after < means that it is being passed as the second argument to the operator, which is inconvenient for eta-conversion. Observe that (<n) is equivalent to (n>), so the following is equivalent to the definition above:

lessThan n = filter (n>)

Now we can use the non-infix form of (>):

lessThan n = filter ((>) n)

And we see from our definition of compose, that if we were to replace filter by f, (>) by g, and n by x, we would have exactly the definition of (.). Thus,

lessThan n = (filter . (>)) n

And now we can apply eta-conversion:

lessThan = filter . (>)

Between operator sectioningThe process of partially applying an infix operator in Haskell by specifying one of its arguments. For example, (+1) is a section of the addition operator with 1 as the second argument. , the compose combinatorA higher-order function that uses only function application and earlier defined combinators to define a result from its arguments. (.), and eta-conversion it is possible to write many functions in point-free form. For example, the flip combinatorA higher-order function that uses only function application and earlier defined combinators to define a result from its arguments. :

flip :: (a -> b -> c) -> b -> a -> c
flip f a b = f b a

can also be useful in reversing the arguments of a function or operator in order to get them into a position such that they can be eta-reduced.

In code written by experienced haskellers it is very common to see functions reduced to point-free form. Does it make code more readable? To experienced haskellers, many times yes. To novices, perhaps not. When to do it is a matter of preference. Experienced haskellers tend to prefer it, they will argue that it reduces functions like the example one above “to their essence”, removing the “unnecessary plumbing” of explicitly named variables. Whether you like it or not, it is worth being familiar with the tricks above, because you will undoubtedly see them used in practice. The other place where point-free styleA way of defining functions without mentioning their arguments. is very useful is when you would otherwise need to use a lambda function.

Some more (and deeper) discussion is available on the Haskell Wiki.

Exercises

  • Refactor the following functions to be point-free. These are clearly extreme examples but is a useful—and easily verified—practice of operator sectioningThe process of partially applying an infix operator in Haskell by specifying one of its arguments. For example, (+1) is a section of the addition operator with 1 as the second argument. , composition and eta-conversion.
g x y = x^2 + y

f a b c = (a+b)*c

Extension: Warning, this one scary This is very non-assessable, and no one will ask anything harder then first two questions

f a b = a*a + b*b

Solutions

g x y = x^2 + y
g x y = (+) (x^2) y -- operator sectioning
g x   = (+) (x^2) -- eta conversion
g x   = (+) ((^2) x) -- operator sectioning
g x   = ((+) . (^2)) x -- composition
g     = (+) . (^2) -- eta conversion

f a b c = (a+b)*c
f a b c = (*) (a + b) c -- operator sectioning
f a b   = (*) (a + b) -- eta conversion
f a b   = (*) (((+) a) b) -- operator sectioning
f a b   = ((*) . ((+) a)) b -- composition
f a     = (*) . ((+) a) -- eta conversion
f a     = ((*) .) ((+) a)
f a     = (((*) . ) . (+)) a -- composition
f       = ((*) . ) . (+) -- eta conversion

Only look at this one if you are curious (very non-assessable, and no one will ask anything harder then first two questions)

f a b = a*a + b*b
f a b = (+) (a * a) (b * b)

Where do we go from here? We need a function which applies the * function to the same argument b Lets invent one:

apply :: (b -> b -> c) -> b -> c
apply f b = f b b

f a b = a*a + b*b
f a b = (+) (a * a) (b * b)
f a b = (+) (apply (*) a) (apply (*) b) -- using our apply function
f a b = ((+) (apply (*) a)) ((apply (*)) b) -- this is in the form f (g x), where f == ((+) (apply (*) a)) and g == (apply (*))

f a b = f (g b)
  where
    f = ((+) (apply (*) a))
    g = (apply (*))

f a b = (((+) (apply (*) a)) . (apply (*))) b -- apply function composition
f a = ((+) (apply (*) a)) . (apply (*)) -- eta conversion
f a = (. (apply (*))) ((+) (apply (*) a))  -- operator sectioning
f a = (. (apply (*))) ((+) . (apply (*)) a) -- composition inside brackets ((+) (apply (*) a))
f a = (. (apply (*))) . ((+) . (apply (*))) a -- composition
f = (. (apply (*))) . ((+) . (apply (*))) -- eta conversion
f = (. apply (*)) . (+) . apply (*) -- simplify brackets

Functor

We’ve been mapping over lists and arrays many times, first in JavaScript:

console> [1,2,3].map(x=>x+1)
[2,3,4]

Now in Haskell:

GHCi> map (\i->i+1) [1,2,3]
[2,3,4]

Or (eta-reduce the lambda to be point-free):

GHCi> map (+1) [1,2,3]
[2,3,4]

Here’s the implementation of map for lists as it’s defined in the GHC standard library:

map :: (a -> b) -> [a] -> [b]
map _ []     = []
map f (x:xs) = f x : map f xs

It’s easy to generalise this pattern to any data structure that holds one or more values: mapping a function over a data structure creates a new data structure whose elements are the result of applying the function to the elements of the original data structure. We have seen examples of generalizing the idea of mapping previously, for example, mapping over a Tree.

In Haskell this pattern is captured in a type classA type system construct in Haskell that defines a set of functions that can be applied to different types, allowing for polymorphic functions. called Functor, which defines a function called fmap.

Prelude> :i Functor
type Functor :: (* -> *) -> Constraint
class Functor f where
  fmap :: (a -> b) -> f a -> f b
...
instance Functor [] -- naturally lists are an instance
instance Functor Maybe -- but this may surprise!
... -- and some other instances we’ll talk about shortly

The first line says that an instances of the FunctorA type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure. typeclass f must be over a type that has the kind (* -> *), that is, their constructors must be parameterised with a single type variable. After this, the class definition specifies fmap as a function that will be available to any instance of FunctorA type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure. and that f is the type parameterA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. for the constructor function, which again, takes one type parameterA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. , e.g. f a as the input to fmap, which returns an f b. While, this may sound complex and abstract, the power of fmap is just applying the idea of a map function to any collection of item(s).

Naturally, lists have an instance:

Prelude> :i []
...
instance Functor [] -- Defined in `GHC.Base'

We can actually look up GHC’s implementation of fmap for lists and we see:

instance Functor [] where
    fmap = map

fmap is defined for other types we have seen, such as a Maybe. Maybes can be considered as list of 0 items (Nothing) or 1 item (Just), and therefore, naturally, we should be able to fmap over a Maybe.

instance  Functor Maybe  where
    fmap _ Nothing       = Nothing
    fmap f (Just a)      = Just (f a)

We can use fmap to apply a function to a Maybe value without needing to unpack it. The true power of fmap lies in its ability to apply a function to value(s) within a context without requiring knowledge of how to extract those values from the context.

GHCi> fmap (+1) (Just 6)
Just 7

This is such a common operation that there is an operator alias for fmap: <$>

GHCi> (+1) <$> (Just 6)
Just 7

Which also works over lists:

GHCi> (+1) <$> [1,2,3]
[2,3,4]

Lists of Maybes frequently arise. For example, the mod operation on integers (e.g. mod 3 2 == 1) will throw an error if you pass 0 as the divisor:

> mod 3 0
*** Exception: divide by zero

We might define a safe modulo function:

safeMod :: Integral a => a-> a-> Maybe a
safeMod _ 0 = Nothing
safeMod numerator divisor = Just $ mod numerator divisor

This makes it safe to apply safeMod to an arbitrary list of Integral values:

> map (safeMod 3) [1,2,0,4]
[Just 0,Just 1,Nothing,Just 3]

But how do we keep working with such a list of Maybes? We can map an fmap over the list:

GHCi> map ((+1) <$>) [Just 0,Just 1,Nothing,Just 3]
[Just 1,Just 2,Nothing,Just 4]

Or equivalently:

GHCi> ((+1) <$>) <$> [Just 0,Just 1,Nothing,Just 3]
[Just 1,Just 2,Nothing,Just 4]

In addition to lists and Maybes, a number of other built-in types have instances of Functor:

GHCi> :i Functor
...
instance Functor (Either a) -- Defined in `Data.Either'
instance Functor IO -- Defined in `GHC.Base'
instance Functor ((->) r) -- Defined in `GHC.Base'
instance Functor ((,) a) -- Defined in `GHC.Base'

The definition for functions (->) might surprise:

instance Functor ((->) r) where
    fmap = (.)

So the composition of functions f and g, f . g, is equivalent to ‘mapping’ f over g, e.g. f <$> g.

GHCi> f = (+1)
GHCi> g = (*2)
GHCi> (f.g) 3
7
GHCi> (f<$>g) 3
7

Functor Laws

We can formalise the definition of FunctorA type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure. with two laws:

The law of identity

∀ x: (id <$> x) ≡ x

The law of composition

∀ f, g, x: (f ∘ g <$> x) ≡ (f <$> (g <$> x))

Note that these laws are not enforced by the compiler when you create your own instances of Functor. You’ll need to test them for yourself. Following these laws guarantees that general code (e.g. algorithms) using fmap will also work for your own instances of Functor.

Let’s make a custom instance of Functor for a simple binary tree type and check that the laws hold. Here’s a simple binary tree datatype:

data Tree a = Empty
            | Leaf a
            | Node (Tree a) a (Tree a)
  deriving (Show)

Note that Leaf is a bit redundant as we could also encode nodes with no children as Node Empty value Empty—but that’s kind of ugly and makes showing our trees more verbose. Also, having both Leaf and Empty provides a nice parallel to Maybe.

Here’s an example tree defined:

tree = Node (Node (Leaf 1) 2 (Leaf 3)) 4 (Node (Leaf 5) 6 (Leaf 7))

And here’s a visualisation of the tree:

Node 4
 ├──Node 2
 |   ├──Leaf 1
 |   └──Leaf 3
 └──Node 6
     ├──Leaf 5
     └──Leaf 7

And here’s the instance of Functor for Tree that defines fmap.

instance Functor Tree where
   fmap :: (a -> b) -> Tree a -> Tree b
   fmap _ Empty = Empty
   fmap f (Leaf v) = Leaf $ f v
   fmap f (Node l v r) = Node (fmap f l) (f v) (fmap f r)

Just as in the Maybe instance above, we use pattern matchingA mechanism in functional programming languages to check a value against a pattern and to deconstruct data. to define a case for each possible constructor in the ADT. The Empty and Leaf cases are very similar to Maybe fmap for Nothing and Just respectively, that is, for Empty we just return another Empty, for Leaf we return a new Leaf containing the application of f to the value x stored in the leaf. The fun one is Node. As for Leaf, fmap f of a Node returns a new Node whose own value is the result of applying f to the value stored in the input Node, but the left and right children of the new node will be the recursive application of fmap f to the children of the input node.

Now we’ll demonstrate (but not prove) that the two laws hold at least for our example tree:

Law of Identity:

> id <$> tree
Node (Node (Leaf 1) 2 (Leaf 3)) 4 (Node (Leaf 5) 6 (Leaf 7))

Law of Composition:

> (+1) <$> (*2) <$> tree
Node (Node (Leaf 3) 5 (Leaf 7)) 9 (Node (Leaf 11) 13 (Leaf 15))
> (+1).(*2) <$> tree
Node (Node (Leaf 3) 5 (Leaf 7)) 9 (Node (Leaf 11) 13 (Leaf 15))

Applicative

The typeclass Applicative introduces a new operator <*> (pronounced “apply”), which lets us apply functions inside a computational context.

ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). is a “subclass” of Functor, meaning that an instance of Applicative can be fmaped over, but ApplicativesA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). also declare (at least) two additional functions, pure and (<*>) (pronounced ‘apply’—but I like calling it “TIE Fighter”):

GHCi> :i Applicative
class Functor f => Applicative (f :: * -> *) where
  pure :: a -> f a
  (<*>) :: f (a -> b) -> f a -> f b

As for Functor all instances of the ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). type-class must satisfy certain laws, which again are not checked by the compiler. ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). instances must comply with these laws to produce the expected behaviour. You can read about the ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). Laws if you are interested, but they are a little more subtle than the basic FunctorA type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure. laws above, and it is not essential to understand them to be able to use <*> in Haskell.

As for Functor, many Base Haskell types are also Applicative, e.g. [], Maybe, IO and (->).

For example, a function inside a Maybe can be applied to a value in a Maybe.

GHCi> Just (+3) <*> Just 2
Just 5

Or a list of functions [(+1),(+2)] to things inside a similar context (e.g. a list [1,2,3]).

> [(+1),(+2)] <*> [1,2,3]
[2,3,4,3,4,5]

Note that lists definition of <*> produces the Cartesian product of the two lists, that is, all the possible ways to apply the functions in the left list to the values in the right list. It is interesting to look at the source for the definition of Applicative for lists on Hackage:

instance Applicative [] where
  pure x    = [x]
  fs <*> xs = [f x | f <- fs, x <- xs]  -- list comprehension

The definition of <*> for lists uses a list comprehension. List comprehensions are a short-hand way to generate lists, using notation similar to mathematical “set builder notation”. The set builder notation here would be: {f(x) | f ∈ fs ∧ x ∈ xs}. In English it means: “the set (Haskell list) of all functions in fs applied to all values in xs”.

A common use-case for ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). is applying a binary (two-parameter) function over two ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). values, e.g.:

> pure (+) <*> Just 3 <*> Just 2
Just 5

So:

  • pure puts the binary function into the applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). (i.e. pure (+) :: Maybe (Num -> Num -> Num)),
  • then <*>ing this function inside over the first Maybe value Just 3 achieves a partial applicationThe process of fixing a number of arguments to a function, producing another function of smaller arity. of the function inside the Maybe. This gives a unary function inside a Maybe: i.e. Just (3+) :: Maybe (Num->Num).
  • Finally, we <*> this function inside a Maybe over the remaining Maybe value.

This is where the name “applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). ” comes from, i.e. Applicative is a type over which a non-unary function may be applied. Note, that the following use of <$> (infix fmap) is equivalent and a little bit more concise:

> (+) <$> Just 3 <*> Just 2
Just 5

This is also called “liftingThe process of applying a function to arguments that are within a context, such as a Functor or Applicative. ” a function over an ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). . Actually, it’s so common that ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). also defines dedicated functions for liftingThe process of applying a function to arguments that are within a context, such as a Functor or Applicative. binary functions (in the GHC.Base module):

> GHC.Base.liftA2 (+) (Just 3) (Just 2)
Just 5

Here’s a little visual summary of ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). and liftingThe process of applying a function to arguments that are within a context, such as a Functor or Applicative. (box metaphor inspired by adit.io):

Applicative Visual Summary

It’s also useful to lift binary data constructors over two ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). values, e.g. for tuples:

> (,) <$> Just 3 <*> Just 2
Just (3, 2)

We can equally well apply functions with more than two arguments over the correct number of values inside ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). contexts. Recall our student data type:

data Student = Student { id::Integer, name::String, mark::Int }

with a ternary constructor:

Student::Integer -> String -> Int -> Student

Let’s say we want to create a student for a given id but we need to look up the name and mark from tables, i.e. lists of key-value pairs: names::[(Integer,String)] and marks::[(Integer,Int)]. We’ll use the function lookup :: Eq a => a -> [(a, b)] -> Maybe b, which will either succeed with Just the result, or fail to find the value for a given key, and return Nothing.

lookupStudent :: Integer -> Maybe Student
lookupStudent sid = Student sid <$> lookup sid names <*> lookup sid marks

Lists are also instances of Applicative. Given the following types:

data Suit = Spade|Club|Diamond|Heart
 deriving (Eq,Ord,Enum,Bounded)

instance Show Suit where
 show Spade = "^"     -- ♠  (closest I could come in ASCII was ^)
 show Club = "&"      -- ♣
 show Diamond = "O"   -- ♦
 show Heart = "V"     -- ♥

data Rank = Two|Three|Four|Five|Six|Seven|Eight|Nine|Ten|Jack|Queen|King|Ace
 deriving (Eq,Ord,Enum,Show,Bounded)

data Card = Card Suit Rank
 deriving (Eq, Ord, Show)

We can make one card using the Card constructor:

GHCi> Card Spade Ace
Card ^ Ace

Or, since both Suit and Rank derive Enum, we can enumerate the full lists of Suits and Ranks, and then lift the Card operator over both lists to create a whole deck:

GHCi> Card <$> [Spade ..] <*> [Two ..]
[Card ^ Two,Card ^ Three,Card ^ Four,Card ^ Five,Card ^ Six,Card ^ Seven,Card ^ Eight,Card ^ Nine,Card ^ Ten,Card ^ Jack,Card ^ Queen,Card ^ King,Card ^ Ace,Card & Two,Card & Three,Card & Four,Card & Five,Card & Six,Card & Seven,Card & Eight,Card & Nine,Card & Ten,Card & Jack,Card & Queen,Card & King,Card & Ace,Card O Two,Card O Three,Card O Four,Card O Five,Card O Six,Card O Seven,Card O Eight,Card O Nine,Card O Ten,Card O Jack,Card O Queen,Card O King,Card O Ace,Card V Two,Card V Three,Card V Four,Card V Five,Card V Six,Card V Seven,Card V Eight,Card V Nine,Card V Ten,Card V Jack,Card V Queen,Card V King,Card V Ace]

Exercise

  • Create instances of Show for Rank and Card such that a deck of cards displays much more succinctly, e.g.:
[^2,^3,^4,^5,^6,^7,^8,^9,^10,^J,^Q,^K,^A,&2,&3,&4,&5,&6,&7,&8,&9,&10,&J,&Q,&K,&A,O2,O3,O4,O5,O6,O7,O8,O9,O10,OJ,OQ,OK,OA,V2,V3,V4,V5,V6,V7,V8,V9,V10,VJ,VQ,VK,VA]
  • Try and make the definition of show for Rank a one-liner using zip and lookup.

Solutions

instance Show Suit where
    show Spade = "^"     -- Represents Spades
    show Club = "&"      -- Represents Clubs
    show Diamond = "O"   -- Represents Diamonds
    show Heart = "V"     -- Represents Hearts

instance Show Rank where
    show Two = "2"
    show Three = "3"
    show Four = "4"
    show Five = "5"
    show Six = "6"
    show Seven = "7"
    show Eight = "8"
    show Nine = "9"
    show Ten = "10"
    show Jack = "J"
    show Queen = "Q"
    show King = "K"
    show Ace = "A"

instance Show Card where
    show (Card s r) = show s ++ show r

To define the show method for Rank as a one-liner using zip and lookup, we can leverage these functions to directly map the Rank constructors to their respective string representations.

instance Show Rank where
    show r = fromMaybe "" $ lookup r (zip [Two .. Ace] ["2", "3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K", "A"])

Different Ways To Apply Functions Cheatsheet

 g x         -- apply function g to argument x
 g $ x       -- apply function g to argument x
 g <$> f x   -- apply function g to argument x which is inside Functor f
 f g <*> f x -- apply function g in Applicative context f to argument x which is also inside f

We saw that functions (->) are FunctorsA type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure. , such that (<$>)=(.). There is also an instance of ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). for functions of input type r. We’ll give the types of the essential functions for the instance:

instance Applicative ((->)r) where
  pure :: a -> (r->a)
  (<*>) :: (r -> (a -> b)) -> (r -> a) -> (r -> b)

This is very convenient for creating point-free implementations of functions which operate on their parameters more than once. For example, imagine our Student type from above has additional fields with breakdowns of marks: e.g. exam and nonExam, requiring a function to compute the total mark:

totalMark :: Student -> Int
totalMark s = exam s + nonExam s

Here’s the point-free version, taking advantage of the fact that exam and nonExam, both being functions of the same input type Student, are both in the same ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). context:

totalMark = (+) <$> exam <*> nonExam

Or equivalently:

totalMark = (+) . exam <*> nonExam

Applicative Exercises

  • Derive the implementations of pure and <*> for Maybe and for functions ((->)r).

Solutions

MaybesA built-in type in Haskell used to represent optional values, allowing functions to return either Just a value or Nothing to handle cases where no value is available.

First lets consider Maybe. The type signature for pure is:

pure :: a -> Maybe a

The idea behind pure is to take the value of type a and put it inside the context. So, we take the value x and put it inside the Just constructor.

pure :: a -> Maybe a
pure x = Just x

A simple way to define this is to consider all possible options of the two parameters, and define the behaviour by following the types

(<*>) :: Maybe (a -> b) -> Maybe a -> Maybe b

(<*>) :: Maybe (a -> b) -> Maybe a -> Maybe b
(<*>) (Just a) (Just b) = Just (a b) -- We can apply the function to the value, we have both!
(<*>) Nothing (Just b) = Nothing -- Do not have the function, so all we can do is return Nothing
(<*>) (Just a) Nothing = Nothing -- Do not have the value, so all we can do is return Nothing
(<*>) Nothing Nothing = Nothing -- Do not have value or function, not much we can do here...

We observe that only one case returns a value, while all other cases, return Nothing, so we can simplify our code using the wildcard _ when pattern matchingA mechanism in functional programming languages to check a value against a pattern and to deconstruct data. .

(<*>) :: Maybe (a -> b) -> Maybe a -> Maybe b
(<*>) (Just a) (Just b) = Just (a b) -- We can apply the function to the value, we have both!
(<*>) _ _ = Nothing -- All other cases, return Nothing

Functions

The type definitions for the function type ((->)r) is a bit more nuanced. When we write ((->) r), we are partially applying the -> type constructor. The -> type constructor takes two type arguments: an argument type and a return type. By supplying only the first argument r, we get a type constructor that still needs one more type to become a complete type.

For a bit of intuition around we can make a function in instance of the applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). instance, you can consider the context is an environment r. The pure function for the reader applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). takes a value and creates a function that ignores the environment and always returns that value. The <*> function for the function instance combines two functions that depend on the same environment.

First, lets consider pure.

pure :: a -> (((->)r) a)

This may look confusing, but if you replace ((->)r) with Maybe, you can see it is essentially the same. Similar to converting prefix functions to infix, we can do the same thing with the type operation here, therefore, this is equivalent to:

pure :: a -> (r -> a)

We can follow the types to write a definition for this:

pure :: a -> (r -> a)
pure a = \r -> a

This definition takes a single parameter a and returns a function. This function, when given any parameter r, will return the original parameter a. Since all functions are curried in Haskell, this is equivalent to:

pure :: a -> (r -> a)
pure a _ = -> a

The function pure helps you create a function that, no matter what the second input is, will always return this first value, this is exactly the K-combinatorA combinator that takes two arguments and returns the first one. .

Reminder the definition for applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). is:

(<*>) :: (f (a -> b)) -> (f a) -> (f b)

For the function applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). , our f is ((->)r)

(<*>) :: (((->) r) (a -> b)) -> (((->) r) a) -> (((->) r) b)

Converting the type signature to use (->) infix rather than prefix

(<*>) :: (r -> (a -> b)) -> (r -> a) -> (r -> b)

For the function body, our function takes two arguments and returns a function of type r -> b.

We have to do some Lego to fit the variables together to get out the correct type b.

(<*>) :: (r -> (a -> b)) -> (r -> a) -> (r -> b)
(<*>) f g = \r -> (f r) (g r)

The function (<*>) takes two functions, one of type r -> (a -> b) and another of type r -> a, and combines them to produce a new function of type r -> b. It does this by applying both functions to the same input r and then applying the result of the first function to the result of the second.

One neat function we can make out of this, we will call apply passes one argument to a binary function twice which can be a useful trick.

apply :: (b -> b -> c) -> b -> c
apply f b = (f <*> (\x -> x)) b

or more simply:

apply :: (b -> b -> c) -> b -> c
apply f = f <*> id

This will allow us to make more functions point-free

square :: Num a => a => a
square = a * a

square a = apply (*) a
square = apply (*)

Alternative

The AlternativeA type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes. typeclass is another important typeclass in Haskell, which is closely related to the ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). typeclass. It introduces a set of operators and functions that are particularly useful when dealing with computations that can fail or have multiple possible outcomes. AlternativeA type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes. is also considered a “subclass” of ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). , and it provides additional capabilities beyond what ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). offers. It introduces two main functions, empty and <|> (pronounced “alt” or “alternativeA type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes. ”)

class Applicative f => Alternative (f :: * -> *) where
  empty :: f a
  (<|>) :: f a -> f a -> f a

empty: This function represents a computation with no result or a failure. It serves as the identity element. For different data types that are instances of AlternativeA type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes. , empty represents an empty container or a failed computation, depending on the context.

(<|>): The <|> operator combines two computations, and it’s used to express alternativesA type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes. . It takes two computations of the same type and returns a computation that will produce a result from the first computation if it succeeds, or if it fails, it will produce a result from the second computation. This operator allows you to handle branching logic and alternativeA type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes. paths in your code.

Like FunctorA type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure. and ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). , instances of the AlternativeA type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes. typeclass must also adhere to specific laws, ensuring predictable behavior when working with alternativesA type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes. . Common instances of the AlternativeA type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes. typeclass include MaybeA built-in type in Haskell used to represent optional values, allowing functions to return either Just a value or Nothing to handle cases where no value is available. and lists ([]). AlternativesA type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes. are also very useful for ParsersA function or program that interprets structured input, often used to convert strings into data structures. , where we try to run first parserA function or program that interprets structured input, often used to convert strings into data structures. , if it fails, we run the second parserA function or program that interprets structured input, often used to convert strings into data structures. .

> Just 2 <|> Just 5
Just 2

> Nothing <|> Just 5
Just 5

Exercise

  • One useful function, which will be coming up throughout the semester is asum with the type definition asum :: Alternative f => [f a] -> f a. Write this function using foldr

Solutions

A naive approach will be to use recursion (recursion is hard).

asum :: Alternative f => [f a] -> f a
asum [] = empty -- When we reach empty list, return the empty alternative
asum (x:xs) = x <|> asum xs -- Otherwise recursively combine the first value and the rest of the list

However, you may recognize this pattern, of recursion to a base case, combining current value with an accumulated value.

This is a classic example of a foldr

Therefore we can write asum simply as:

asum :: Alternative f => [f a] -> f a
asum = foldr (<|>) empty

A simple Applicative Functor for Parsing

As we will discuss in more detail later, a parserA function or program that interprets structured input, often used to convert strings into data structures. is a program which takes some structured input and does something with it. When we say “structured input” we typically mean something like a string that follows strict rules about its syntaxThe set of rules that defines the combinations of symbols that are considered to be correctly structured statements or expressions in a computer language. , like source code in a particular programming language, or a file format like JSON. A parserA function or program that interprets structured input, often used to convert strings into data structures. for a given syntaxThe set of rules that defines the combinations of symbols that are considered to be correctly structured statements or expressions in a computer language. is a program which you run over some input and if the input is valid, it will do something sensible with it (like give us back some data), or fail: preferably in a way that we can handle gracefully.

In Haskell, sophisticated parsersA function or program that interprets structured input, often used to convert strings into data structures. are often constructed from simple functions which try to read a certain element of the expected input and either succeed in consuming that input, returning a tuple containing the rest of the input string and the resultant data, or they fail producing nothing. We’ve already seen one type which can be used to encode success or failure, namely Maybe. Here’s the most trivial parserA function or program that interprets structured input, often used to convert strings into data structures. function I can think of. It tries to take a character from the input stream and either succeeds consuming it or fails if it’s given an empty string:

-- >>> parseChar "abc"
-- Just ("bc",'a')
-- >>> parseChar ""
-- Nothing
parseChar :: String -> Maybe (String, Char)
parseChar "" = Nothing
parseChar (c:rest) = Just (rest, c)

And here’s one to parse Ints off the input stream. It uses the reads function from the PreludeThe default library loaded in Haskell that includes basic functions and operators. :

-- >>> parseInt "123+456"
-- Just ("+456",123)
-- >>> parseInt "xyz456"
-- Nothing
parseInt :: String -> Maybe (String, Int) 
parseInt s = case reads s of     
  [(x, rest)] -> Just (rest, x)
  _           -> Nothing

So now we could combine these to try to build a little calculator language (OK, all it can do is add two integers, but you get the idea):

-- >>> parsePlus "123+456"
-- Just ("",579)
parsePlus :: String -> Maybe (String, Int)
parsePlus s =
    case parseInt s of
        Just (s', x) -> case parseChar s' of
            Just (s'', '+') -> case parseInt s'' of
                Just (s''',y) -> Just (s''',x+y)
                Nothing -> Nothing
            Nothing -> Nothing
        Nothing -> Nothing

But that’s not very elegant and Haskell is all about elegant simplicity. So how can we use Haskell’s typeclass system to make parsersA function or program that interprets structured input, often used to convert strings into data structures. that are more easily combined? We’ve seen how things that are instances of the Functor and Applicative typeclasses can be combined—so let’s make a type definition for parsersA function or program that interprets structured input, often used to convert strings into data structures. and then make it an instance of Functor and Applicative. Here’s a generic type for parsersA function or program that interprets structured input, often used to convert strings into data structures. :

newtype Parser a = Parser (String -> Maybe (String, a))

We can now make concrete parsersA function or program that interprets structured input, often used to convert strings into data structures. for Int and Char using our previous functions, which conveniently already had functions in the form (String -> Maybe (String, a)):

char :: Parser Char
char = Parser parseChar
int :: Parser Int
int = Parser parseInt

And here’s a simple generic function we can use to run these parsersA function or program that interprets structured input, often used to convert strings into data structures. . All this does, is extract the inner function p from the Parser constructor

-- >>> parse int "123+456"
-- Just ("+456",123)
parse :: Parser a -> String -> Maybe (String, a)
parse (Parser p) = p

And a parserA function or program that interprets structured input, often used to convert strings into data structures. which asserts the next character on the stream is the one we are expecting:

is :: Char -> Parser Char
is c = Parser $
  \inputString -> case parse char inputString of
    Just (rest, result) | result == c -> Just (rest, result)
    _ -> Nothing

Aside: How do we get to that parser?

The is function constructs a parserA function or program that interprets structured input, often used to convert strings into data structures. that succeeds and consumes a character from the input string if it matches the specified character c, otherwise it fails.

-- >>> parse (is '+') "+456"
-- Just ("456",'+')
-- >>> parse (is '-') "+456"
-- Nothing
is :: Char -> Parser Char
is c = Parser $ \inputString ->
  case inputString of
    [] -> Nothing
    (x:xs) -> case x == c of
      True  -> Just (xs, x)
      False -> Nothing

However, this is quickly becoming very deeply nested, lets use our previous char parserA function or program that interprets structured input, often used to convert strings into data structures. to ensure correct behaviour for the empty string, rather than duplicating that logic.

-- >>> parse (is '+') "+456"
-- Just ("456",'+')
-- >>> parse (is '-') "+456"
-- Nothing
is :: Char -> Parser Char
is c = Parser $
  \inputString -> case parse char inputString of
    Just (rest, result)
      | result == c -> Just (rest, result)
      | otherwise = Nothing
    _ -> Nothing

In this example, the otherwise = Nothing guard is not needed, as our case statement can handle that in the wildcard statement

is :: Char -> Parser Char
is c = Parser $
  \inputString -> case parse char inputString of
    Just (rest, result) | result == c -> Just (rest, result)
    _ -> Nothing

By making Parser an instance of Functor we will be able to map functions over the result of a parse, this is very useful! For example, consider the int parserA function or program that interprets structured input, often used to convert strings into data structures. , which parses a string to an integer, and if we want to apply a function to the result, such as adding 1 (+1), we can fmap this over the parserA function or program that interprets structured input, often used to convert strings into data structures. .

add1 :: Parser Int
add1 = (+1) <$> int

We can now use this to parse a string “12”, and get the result 13. parse add1 "12" will result in 13

The fmap function for the Functor instance of Parser needs to apply the parserA function or program that interprets structured input, often used to convert strings into data structures. to an input string and apply the given function to the result of the parse, i.e.:

instance Functor Parser where
  fmap f (Parser p) = Parser $
    \i -> case p i of 
      Just (rest, result) -> Just (rest, f result)
      _ -> Nothing

That definition may be difficult to understand, on first look, but we take apply the parserA function or program that interprets structured input, often used to convert strings into data structures. p and apply the function f to the result of the parsing, i.e., we apply the parserA function or program that interprets structured input, often used to convert strings into data structures. p and if it succeeds (returns a Just) we apply the function f to the result.

However, we can take advantage of the fact that the Tuple returned by the parse function is also an instance of Functor to make the definition more succinct. That is, we are applying the function f to the second item of a tuple—that is exactly what the fmap for the Functor instance of a Tuple does! So we can rewrite to use the Tuple fmap, or rather its alias (<$>):

instance Functor Parser where
  fmap f (Parser p) = Parser $
    \i -> case p i of 
      Just (rest, result) -> Just (f <$> (rest, result))
      _ -> Nothing

Carefully examining this, what we are doing is applying (f <$>) if the result is a Just, or ignoring if the result is Nothing. This is exactly what the Maybe instance of Functor does, so we can fmap over the Maybe also:

instance Functor Parser where
  fmap f (Parser p) = Parser (\i -> (f <$>) <$> p i )

Let’s try rearrange to make it point point-free, eliminating the lambda: First, let’s add some brackets, to make the evaluation order more explicit.

instance Functor Parser where
  fmap f (Parser p) = Parser (\i -> ((f <$>) <$>) (p i))

This is now in the form (f . g) i) where f is equal to ((f <$>) <$>) and g is equal to p. Therefore:

instance Functor Parser where
  fmap f (Parser p) = Parser (\i -> (((f <$>) <$>) . p) i)

And, if we eta-reduce:

instance Functor Parser where
  fmap f (Parser p) = Parser (((f <$>) <$>) . p)

The last thing we notice is that the Functor instance for functions is defined as compose. Therefore, we have finally reached the end of our journey and can re-write this as follows.

-- >>> parse ((*2) <$> int) "123+456"
-- Just ("+456",246)
instance Functor Parser where
  fmap f (Parser p) = Parser (((f <$>) <$>) <$> p)

The whacky triple-nested application of <$> comes about because the result type a in our Parser type is nested inside a Tuple ((,a)), nested inside a Maybe, nested inside function (->r). So now we can map (or fmap, to be precise) a function over the value produced by a Parser. For example:

> parse ((+1)<$>int) "1bc"
Just ("bc",2)

So (+1)<$>int creates a new Parser which parses an int from the input stream and adds one to the value parsed (if it succeeds). Behind the scenes, using the implementation above, the Parser’s instance of FunctorA type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure. is effectively liftingThe process of applying a function to arguments that are within a context, such as a Functor or Applicative. over three additional layers of nested types to reach the Int value, i.e.:

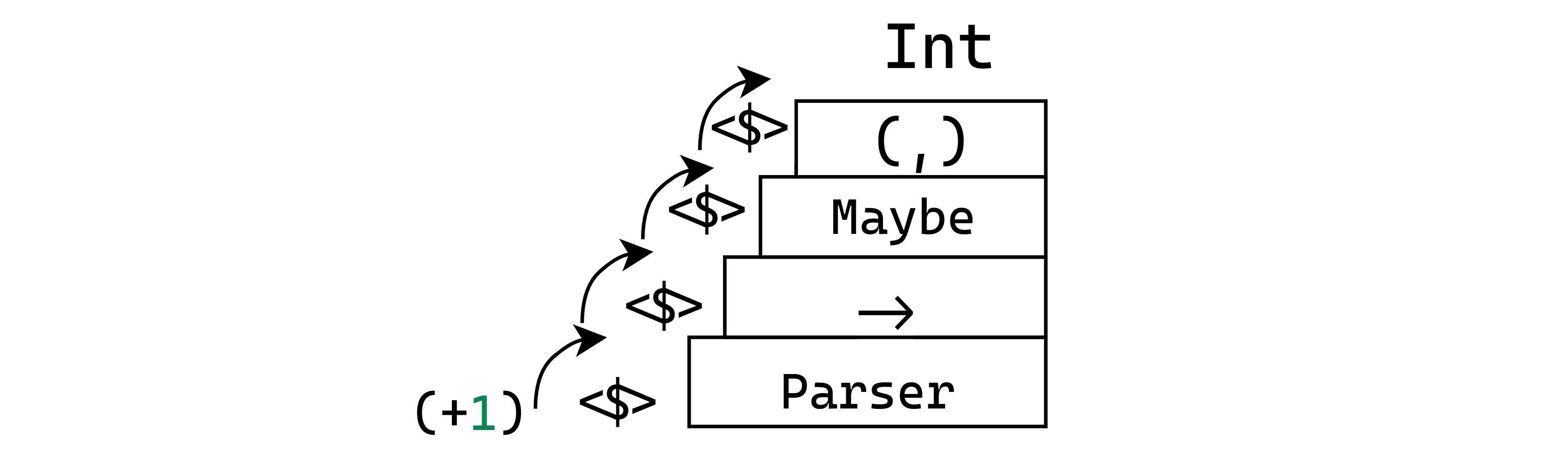
Applicative Visual Summary

Just as we have seen before, making our Parser an instance of Applicative is going to let us do nifty things like liftingThe process of applying a function to arguments that are within a context, such as a Functor or Applicative. a binary function over the results of two Parsers. Thus, instead of implementing all the messy logic of connecting two ParsersA function or program that interprets structured input, often used to convert strings into data structures. to make plus above, we’ll be able to lift (+) over two Parsers.

Now the definition for the Applicative is going to stitch together all the messy bits of handling both the Just and Nothing cases of the Maybe that we saw above in the definition of plus, abstracting it out so that people implementing parsersA function or program that interprets structured input, often used to convert strings into data structures. like plus won’t have to:

instance Applicative Parser where
  pure a = Parser (\b -> Just (b, a))

  (Parser f) <*> (Parser g) = Parser $
    \i -> case f i of                                       -- note that this is just
      Just (r1, p1) -> case g r1 of                         -- an abstraction of the
        Just (r2, p2) -> Just (r2, p1 p2)                   -- logic we saw in `plus`
        Nothing       -> Nothing
      Nothing -> Nothing

All that pure does is put the given value on the right side of the tuple.

The key insight for this applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). instance is that we first use f (the parserA function or program that interprets structured input, often used to convert strings into data structures. on the LHS of <*>). This consumes input from i giving back the remaining input in r1. We then run the second parserA function or program that interprets structured input, often used to convert strings into data structures. g on the RHS of <*> on r1 (the remaining input).

The main take-away message is that <*> allows us to combine two parsersA function or program that interprets structured input, often used to convert strings into data structures. in sequence, that is, we can run the first one and then the second one.

Let’s walk through a concrete example of this.

> charIntPairParser = (,) <$> char <*> int
> parse charIntPairParser "a12345b"
Just ("b",('a',12345))

As both <$> and <*> have the same precedence, firstly (,) <$> char will be evaluated, the result will be then applied to int.

So how does (,) <$> char work? Well, we parse a character and then make that character the first item of a tuple, therefore:

> charPairParser = (,) <$> char
> :t charPairParser
charPairParser :: Parser (b -> (Char, b))

So for the applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). instance the LHS will be the charPairParser and the RHS will be int. That is, first step in applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). parsing is to parse the input i using the LHS parserA function or program that interprets structured input, often used to convert strings into data structures. , what we called here charPairParser. This will match the Just (r1, p1) case where it will be equal to Just ("12345b", ('a',)). Therefore, r1 is equal to the unparsed portion of the input 12345b and the result is a tuple partially applied ('a', ).

We then run the second parserA function or program that interprets structured input, often used to convert strings into data structures. int on the remaining input "12345b". This will match the Just (r2, p2) case where it will be equal to Just ("b", 12345), where r2 is equal to the remaining input "b" and p2 is equal to "12345"

We then return Just (r2, p1 p2), which will evaluate to Just ("b", ('a',12345)).

Using the <*> operator we can make our calculator magnificently simple:

-- >>> parse plus "123+456"
-- Just ("",579)
plus :: Parser Int
plus = (+) <$> int <*> (is '+' *> int)

Note that we make use of a different version of the applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). operator here: *>. Note also that we didn’t have to provide an implementation of *> - rather, the typeclass system picks up a default implementation of this operator (and a bunch of other functions too) from the base definition of Applicative. These default implementations are able to make use of the <*> that we provided for our instance of Applicative for Parser.

Prelude> :t (*>)
(*>) :: Applicative f => f a -> f b -> f b

So compared to <*> which took a function inside the Applicative as its first parameter which is applied to the value inside the Applicative of its second parameter, the *> carries through the effect of the first Applicative, but doesn’t do anything else with the value. You can think of it as a simple chaining of effectful operations: “do the first effectful thing, then do the second effectful thing, but give back the result of the second thing only”.

In the context of the Parser instance when we do things like (is '+' *> int), we try the is. If it succeeds then we carry on and run the int. But if the is fails, execution is short circuited and we return Nothing. There is also a flipped version of the operator which works the other way:

Prelude> :t (<*)
(<*) :: Applicative f => f a -> f b -> f a

So we could have just as easily implement the plus parserA function or program that interprets structured input, often used to convert strings into data structures. :

-- >>> parse plus "123+456"
-- Just ("",579)
plus :: Parser Int
plus = (+) <$> int <* is '+'  <*> int

Obviously, the above is not a fully featured parsing system. A real parserA function or program that interprets structured input, often used to convert strings into data structures. would need to give us more information in the case of failure, so a Maybe is not really a sufficiently rich type to package the result. Also, a real language would need to be able to handle alternativesA type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes. - e.g. minus or plus, as well as expressions with an arbitrary number of terms. We will revisit all of these topics with a more feature rich set of parserA function or program that interprets structured input, often used to convert strings into data structures. combinatorsA higher-order function that uses only function application and earlier defined combinators to define a result from its arguments. later.

Left and Right Applicatives

We briefly introduced both (<*) and (*>) but lets deep dive in to why these functions are so useful. The full type definitions are:

(<*) :: Applicative f => f a -> f b -> f a
(*>) :: Applicative f => f a -> f b -> f b

A more intuitive look at these would be:

  • (<*): Executes two actions, but only returns the result of the first action.
  • (*>): Executes two actions, but only returns the result of the second action.

The key term here is action, we can consider the action of our parserA function or program that interprets structured input, often used to convert strings into data structures. as doing the parsing

A definition of (<*) is

(<*) :: Applicative f => f a -> f b -> f a
(<*) fa fb = liftA2 (\a b -> a) fa fb

Where liftA2 = f <$> a <*> b

Let’s relate this to our parsing, and how this executes the two actions. We will consider the example of parsing something in the form of “123+”, wanting to parse the number and ignore the “+”. The execution order will be changed around a little bit, hoping to provide some intuition in to these functions.

So, we can use our “<*” to ignore the second action, i.e., int <* (is '+').

Plugging this in to liftA2 definition:

liftA2 (\a _ -> a) int (is '+')
(\a b -> a) <$> int <*> (is '+') -- from the liftA2 definition
((\a b -> a) <$> int) <*> (is '+') -- we will complete the functor operator first

Recall the definition of Functor for parsing:

instance Functor Parser where
  fmap f (Parser p) = Parser $
    \i -> case p i of
      Just (rest, result) -> Just (rest, f result)
      _ -> Nothing

So, in this scenario our function f is (\a b -> a) and our (Parser p) is the int parserA function or program that interprets structured input, often used to convert strings into data structures. . i is the input string “123+”.

Therefore, (\a b -> a) <$> int will result in Just ("+", (\a b -> a) 123)

Now, we want need to consider the second half, which is

Just ("+", (\a b -> a) 123) being applied to (is '+')

The applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). definition says to apply the second parserA function or program that interprets structured input, often used to convert strings into data structures. is '+' to the remaining input, and apply the result to the function inside the RHS of the tuple.

Therefore, after applying this parserA function or program that interprets structured input, often used to convert strings into data structures. , it will result in: Just ("", (\a b -> a) 123 "+"). Finally, we will apply the function call to ignore the second value, finally resulting in: Just ("", 123). But the key point, is we still executed the is '+' but we ignored the value. That is the beauty of using our <* and *> to ignore results, while still executing actions

Glossary

Operator Sectioning: The process of partially applying an infix operator in Haskell by specifying one of its arguments. For example, (+1) is a section of the addition operator with 1 as the second argument.

Compose Operator: Represented as (.) in Haskell, it allows the composition of two functions, where the output of the second function is passed as the input to the first function.

Point-Free Code: A style of defining functions without mentioning their arguments explicitly. This often involves the use of function composition and other combinators.

Functor: A type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure.

Applicative: A type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>).

Lifting: The process of applying a function to arguments that are within a context, such as a Functor or Applicative.

Alternative: A type class in Haskell that extends Applicative, introducing the empty and <|> functions for representing computations that can fail or have multiple outcomes.

Parser: A function or program that interprets structured input, often used to convert strings into data structures.

Parser Combinator: A higher-order function that takes parsers as input and returns a new parser as output. Parser combinators are used to build complex parsers from simpler ones.