Learning Outcomes

Algebraic Data Types (ADTs)

We can declare custom types for data in Haskell using the data keyword. Consider the following declaration of our familiar cons list:

data ConsList = Nil | Cons Int ConsList

The | operator looks rather like the union typeA TypeScript construct that allows a variable to hold values of multiple specified types, separated by the | symbol. operator in TypeScript, and indeed it serves a similar purpose. Here, a ConsList is defined as being a composite type, composed of either Nil or a Cons of an Int value and another ConsList. This is called an “algebraic data type” because | is like an “or”, or algebraic “sum” operation for combining elements of the type while separating them with a space is akin to “and” or a “product” operation.

Note that neither Nil or Cons are built in. They are simply labels for constructor functions for the different versions of a ConsList node. You could equally well call them EndOfList and MakeList or anything else that’s meaningful to you. Nil is a function with no parameters, Cons is a function with two parameters. Int is a built-in primitive type for limited-precision integers.

Now we can create a small list like so:

l = Cons 1 $ Cons 2 $ Cons 3 Nil

Aside: data vs newtype

We can construct a type UserId with one parameter, Int

data UserId = UserId Int
newtype UserId = UserId Int

These are almost identical, and we can use them both equivallentally, e.g.,

student :: UserId
student = UserId 1337

The newtype keyword is used to define a type that has exactly one constructor with exactly one field. It is primarily used for creating a distinct type from an existing type with zero runtime overhead. This can be useful for adding type safety to your code by creating new types that are distinct from their underlying types or giving types a greater semantic meaning, e.g., a UserId compared to an Int.

The data keyword is used to define an algebraic data type (ADT). This allows for the creation of complex data structures that can have multiple constructors. Each constructor can take zero or more arguments, and these arguments can be of any type.

Pattern Matching

In Haskell, we can define multiple versions of a function to handle the instances of an algebraic data types(or ADTs) Custom data types in Haskell defined using the data keyword, allowing the combination of different types into one composite type using the | operator. . This is done by providing a pattern in the parameter list of the function definition, in the form of an expression beginning with the constructor of the data instance (e.g. Cons or Nil) and variable names which will be bound to the different fields of the data instance.

For example, we can create a function to determine a ConsList’s length using pattern matchingA mechanism in functional programming languages to check a value against a pattern and to deconstruct data. ; to not only create different definitions of the function for each of the possible instances of a ConsList, but also to destructure the non-empty Cons:

consLength :: ConsList -> Int
consLength Nil = 0
consLength (Cons _ rest) = 1 + consLength rest

Since we don’t care about the head value in this function, we match it with _, an unnamed variable, which effectively ignores it. Note that another way to conditionally destructure with pattern matchingA mechanism in functional programming languages to check a value against a pattern and to deconstruct data. is using a case statement.

Note that such a definition for lists is made completely redundant by Haskell’s wonderful built-in lists, where [] is the empty list, and : is an infix cons operator. We can pattern match the empty list or destructure (head:rest), e.g.:

intListLength :: [Int] -> Int -- takes a list of Int as input and returns an Int
intListLength [] = 0
intListLength (_:rest) = 1 + intListLength rest

Type Parameters and Polymorphism

Similar to TypeScript, Haskell provides parametric polymorphismA type of polymorphism where functions or data types can be written generically so that they can handle values uniformly without depending on their type. . That is, the type definitions for functions and data structures (defined with data like the ConsList above) can have type parametersA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. (AKA type variables). For example, the definition intListLength above is defined to only work with lists with Int elements. This seems a silly restriction because in this function we don’t actually do anything with the elements themselves. Below, we introduce the type parameterA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. a so that the length function will able to work with lists of any type of elements.

length :: [a] -> Int -- a is a type parameter
length [] = 0
length (_:rest) = 1 + length rest

The following visual summary shows pair data structures with accessor functions fst and sec defined using Record SyntaxAn alternate way to define data structures in Haskell with named fields, automatically creating accessor functions for those fields. with varying degrees of type flexibility, and compared with the equivalent TypeScript generic notation:

  • Hard-coded for Int pairs only
  • with one type parameterA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. (by convention called a in Haskell, and T in TypeScript)
  • with two type parametersA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. such that the two elements may be different types

Polymorphism Summary

Type Kinds

GHCi allows you to use the :kind (or :k) command to interrogate the Kind of types – think of it as “meta information” about types and their type parametersA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. . The kind syntaxThe set of rules that defines the combinations of symbols that are considered to be correctly structured statements or expressions in a computer language. indicates the arity or number of type parametersA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. a type has. Note that it is like the syntaxThe set of rules that defines the combinations of symbols that are considered to be correctly structured statements or expressions in a computer language. for function types (with the ->), you can think of it as information about what is required in terms of type parametersA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. to instantiate the type. If the constructor takes no type parametersA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. the kind is just *, (it returns a type), *->* if it takes one type parameterA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. , *->*->* for two type parametersA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. and so on.

Polymorphism Summary

Another sort of “kind” are for type classesA way in Haskell to associate functions with types, similar to TypeScript interfaces. They define a set of functions that must be available for instances of those type classes. which we will introduce more properly in a moment. For example, the “kind” for the Ord type classA type system construct in Haskell that defines a set of functions that can be applied to different types, allowing for polymorphic functions. (the class of things that are Orderable and which we came across in our simple implementation of quicksort) is:

> :k Ord
Ord :: * -> Constraint

This tells us that Ord takes one type parameterA placeholder for a type that is specified when a generic function or class is used, allowing for type-safe but flexible code. (for example it could be an Int or other numeric type, or something more complex like the Student type below), and returns a Constraint rather than an actual type. Such a constraintA restriction on type parameters in Haskell, specifying that a type must belong to a certain type class. is used to narrow the set of types to which a function may be applied, just as we saw Ord being used as the type constraintA restriction on type parameters in Haskell, specifying that a type must belong to a certain type class. for sort:

> :t sort
sort :: Ord t => [t] -> [t]

Record Syntax

Consider the following simple record data type:

data Student = Student Int String Int

A Student has three fields, mysteriously typed Int, String and Int. Let’s say my intention in creating the above data type was to store a student’s id, name and mark. I would create a record like so:

> t = Student 123 "Tim" 95

Here’s how one would search for the student with the best mark:

best :: [Student] -> Student -> Student
best [] b = b
best (a@(Student _ _ am):rest) b@(Student _ _ bm) =
  if am > bm
  then best rest a
  else best rest b

The @ notation, as in b@(Student _ _ bm) stores the record itself in the variable b but also allows you to unpack its elements, e.g. bm is bound to mark.

To get the data out of a record I would need to either destructure using pattern matchingA mechanism in functional programming languages to check a value against a pattern and to deconstruct data. , as above, every time, or create some accessor functions:

id (Student n _ _) = n
name (Student _ n _) = n
mark (Student _ _ n) = n
> name t
"Tim"

It’s starting to look a bit like annoying boilerplate code. Luckily, Haskell has another way to define such record types, called record syntaxAn alternate way to define data structures in Haskell with named fields, automatically creating accessor functions for those fields. :

data Student = Student { id::Int, name::String, mark::Int }

This creates a record type in every way the same as the above, but the accessor functions id, name and mark are created automatically.

Typeclasses

Haskell uses “type classesA way in Haskell to associate functions with types, similar to TypeScript interfaces. They define a set of functions that must be available for instances of those type classes. ” as a way to associate functions with types. A type classA type system construct in Haskell that defines a set of functions that can be applied to different types, allowing for polymorphic functions. is like a promise that a certain type will have specific operations and functions available. You can think of it as being similar to a TypeScript interfaceA TypeScript construct that defines the shape of an object, specifying the types of its properties and methods. .

Despite the name however, it is not like an ES6/TypeScript class, since a Haskell type classA type system construct in Haskell that defines a set of functions that can be applied to different types, allowing for polymorphic functions. does not actually give definitions for the functions themselves, only their type signatures.
The function bodies are defined in “instances” of the type classA type system construct in Haskell that defines a set of functions that can be applied to different types, allowing for polymorphic functions. . A good starting point for gaining familiarity with type classesA way in Haskell to associate functions with types, similar to TypeScript interfaces. They define a set of functions that must be available for instances of those type classes. is seeing how they are used in the standard Haskell preludeThe default library loaded in Haskell that includes basic functions and operators. . From GHCi we can ask for information about a specific typeclass with the :i command, for example, Num is a typeclass common to numeric types:

GHCi> :i Num
class Num a where   
  (+) :: a -> a -> a
  (-) :: a -> a -> a
  (*) :: a -> a -> a
  negate :: a -> a
  abs :: a -> a
  signum :: a -> a
  fromInteger :: Integer -> a
  {-# MINIMAL (+), (*), abs, signum, fromInteger, (negate | (-)) #-}
        -- Defined in `GHC.Num'
instance Num Word -- Defined in `GHC.Num'
instance Num Integer -- Defined in `GHC.Num'
instance Num Int -- Defined in `GHC.Num'
instance Num Float -- Defined in `GHC.Float'
instance Num Double -- Defined in `GHC.Float'

The first line (beginning class) tells us that for a type to be an instance of the Num typeclass, it must provide the operators +, * and the functions abs, signum and fromInteger, and either (-) or negate. The last is an option because a default definition exists for each in terms of the other. The last five lines (beginning with “instance”) tell us which types have been declared as instances of Num and hence have definitions of the necessary functions. These are Word, Integer, Int, Float and Double. Obviously this is a much more finely grained set of types than JavaScript’s universal “number” type. This granularity allows the type system to guard against improper use of numbers that might result in loss in precision or division by zero.

The main numeric type we will use in this course is Int, i.e. fixed-precision integers.

Note some obvious operations we would likely need to perform on numbers that are missing from the Num typeclass. For example, equality checking. This is defined in a separate type classA type system construct in Haskell that defines a set of functions that can be applied to different types, allowing for polymorphic functions. Eq, that is also instanced by concrete numeric types like Int:

> :i Eq
class Eq a where
  (==) :: a -> a -> Bool
  (/=) :: a -> a -> Bool
  {-# MINIMAL (==) | (/=) #-}
...
instance Eq Int
...

Note again that instances need implement only == or /= (not equal to), since each can be easily defined in terms of the other. Still we are missing some obviously important operations, e.g., what about greater-than and less-than? These are defined in the Ord type classA type system construct in Haskell that defines a set of functions that can be applied to different types, allowing for polymorphic functions. :

> :i Ord
class Eq a => Ord a where
  compare :: a -> a -> Ordering
  (<) :: a -> a -> Bool
  (<=) :: a -> a -> Bool
  (>) :: a -> a -> Bool
  (>=) :: a -> a -> Bool
  max :: a -> a -> a
  min :: a -> a -> a
  {-# MINIMAL compare | (<=) #-} 

-- The compare function returns an Ordering:
> :i Ordering
data Ordering = LT | EQ | GT

A custom data type can be made an instance of Ord by implementing either compare or <=. The definition Eq a => Ord a means that anything that is an instance of Ord must also be an instance of Eq. Thus, typeclasses can build upon each other into rich hierarchies:

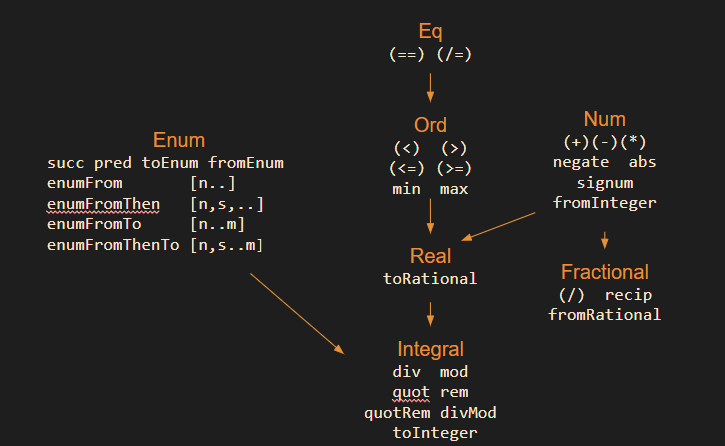
Numeric Typeclasses

Creating custom instances of type classes

If we have our own data types, how can we make standard operations like equality and inequality testing work with them? Luckily, the most common type classesA way in Haskell to associate functions with types, similar to TypeScript interfaces. They define a set of functions that must be available for instances of those type classes. can easily be instanced automatically through the deriving keyword. For example, if we want to define a Suit type for a card game we can automatically generate default instances of the functions (and operators) associated with Equality testing, Ordinal comparisons, Enumerating the different possible values of the type, and Showing them (or converting them to string):

data Suit = Spade|Club|Diamond|Heart
 deriving (Eq,Ord,Enum,Show)

> Spade < Heart
True

The Show typeclass allows the data to be converted to strings with the show function (e.g. so that GHCi can display it). The Enum typeclass allows enumeration, e.g.:

> [Spade .. Heart]
[Spade,Club,Diamond,Heart]

We can also create custom instances of typeclasses by providing our own implementation of the necessary functions, e.g.:

instance Show Suit where
 show Spade = "^"     -- OK, these characters are not
 show Club = "&"      -- brilliant approximations of the
 show Diamond = "O"   -- actual playing card symbols ♠ ♣ ♦ ♥
 show Heart = "V"     -- but GHCi support for unicode 
                      -- characters is a bit sketch
> [Spade .. Heart]
[^,&,O,V]

Maybe

Another important built-in type is Maybe:

> :i Maybe
data Maybe a = Nothing | Just a

All the functions we have considered so far are assumed to be total. That is, the function provides a mapping for every element in the input type to an element in the output type. Maybe allows us to have a sensible return-type for partial functions, that is, functions which do not have a mapping for every input:

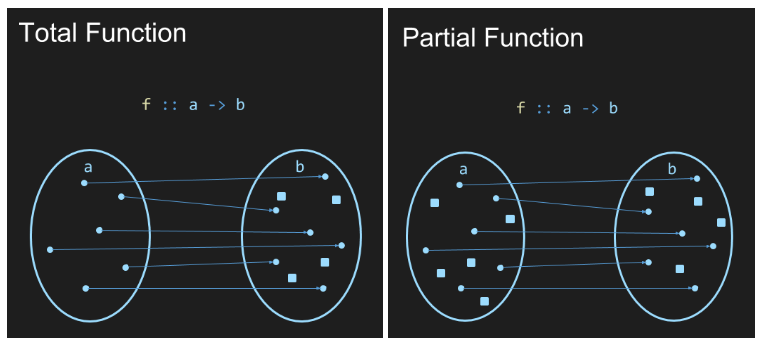
Total and Partial Functions

For example, the built-in function lookup can be used to search a list of key-value pairs, and fail gracefully by returning Nothing if there is no matching key.

phonebook :: [(String, String)]
phonebook = [ ("Bob",   "01788 665242"), ("Fred",  "01624 556442"), ("Alice", "01889 985333") ]

> :t lookup
lookup :: Eq a => a -> [(a, b)] -> Maybe b

> lookup "Fred" phonebook
Just "01624 556442"

> lookup "Tim" phonebook
Nothing

We can use pattern matchingA mechanism in functional programming languages to check a value against a pattern and to deconstruct data. to extract values from a Maybe (when we have Just a value), or to perform some sensible default behaviour when we have Nothing.

printNumber :: String -> IO ()
printNumber name = msg $ lookup name phonebook
where
   msg (Just number)  = print number
   msg Nothing        = print $ name ++ " not found in database"

*GHCi> printNumber "Fred"
"01624 556442"
*GHCi> printNumber "Tim"
"Tim not found in database"

We can also do this using a case statement.

printNumber :: String -> IO ()
printNumber name = msg $ lookup name phonebook
where
   msg value = case value of
    (Just number) -> print number
    _             -> print $ name ++ " not found in database"

Here we use the wildcard _ to match any other possible value, in this case, there is only one other value, Nothing.

Glossary

Algebraic Data Types: (or ADTs) Custom data types in Haskell defined using the data keyword, allowing the combination of different types into one composite type using the | operator.

Record Syntax: An alternate way to define data structures in Haskell with named fields, automatically creating accessor functions for those fields.

Type Classes: A way in Haskell to associate functions with types, similar to TypeScript interfaces. They define a set of functions that must be available for instances of those type classes.

Constraint: A restriction on type parameters in Haskell, specifying that a type must belong to a certain type class.

Type Kind: Meta-information about types and their type parameters in Haskell, indicating the number of type parameters a type has and the type it returns.

Maybe: A built-in type in Haskell used to represent optional values, allowing functions to return either Just a value or Nothing to handle cases where no value is available.

Total Functions: Functions that provide a mapping for every element in the input type to an element in the output type.

Partial Functions: Functions that do not have a mapping for every input, potentially failing for some inputs.