Learning Outcomes

  • Develop a monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. to thread an implicit state parameter through otherwise pure functionsA function that always produces the same output for the same input and has no side effects.
  • Understand that this monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. is generalisable to threading any type of state through a sequence of operations
  • Be aware of the related libraries: System.Random and Control.Monad.State.

Pseudo Random Number Sequences

Pseudorandom number generators create a sequence of unpredictable numbers. The following function generates the next element in a pseudorandom sequence from a previous seed.

type Seed = Int

nextSeed :: Seed -> Seed
nextSeed prevSeed = (a*prevSeed + c) `mod` m
  where -- Parameters for linear congruential RNG.
    a = 1664525
    c = 1013904223
    m = 2^32

From a given seed in the pseudorandom sequence we can generate a number in a specified range.

-- | Generate a number between `l` and `u`, inclusive.
genRand :: Int -> Int -> Seed -> Int
genRand l u seed = seed `mod` (u-l+1) + l

For example:

-- | Roll a six-sided die once.
-- >>> rollDie1 123
-- (5,1218640798)
-- >>> rollDie1 1218640798
-- (4,1868869221)
-- >>> rollDie1 1868869221
-- (1,166005888)
rollDie1 :: Seed -> (Seed, Int)
rollDie1 s =
  let s' = nextSeed s
      n = genRand 1 6 s'
  in (s', n)

And if we want a sequence of dice rolls:

-- | Roll a six-sided die `n` times.
-- >>> diceRolls1 3 123
-- ([5,4,1],166005888)
diceRolls1 :: Int -> Seed -> (Seed, [Int])
diceRolls1 0 s = ([], s)
diceRolls1 n s =
  let (s', r) = rollDie1 s
      (s'', rolls) = diceRolls1 (n-1) s'
  in (s'', r:rolls)

But keeping track of the various seeds (s,s',s'') is tedious and error prone. Let’s invent a monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. which manages the seed for us. The seed will be threaded through all of our functions implicitly in the monadic return type.

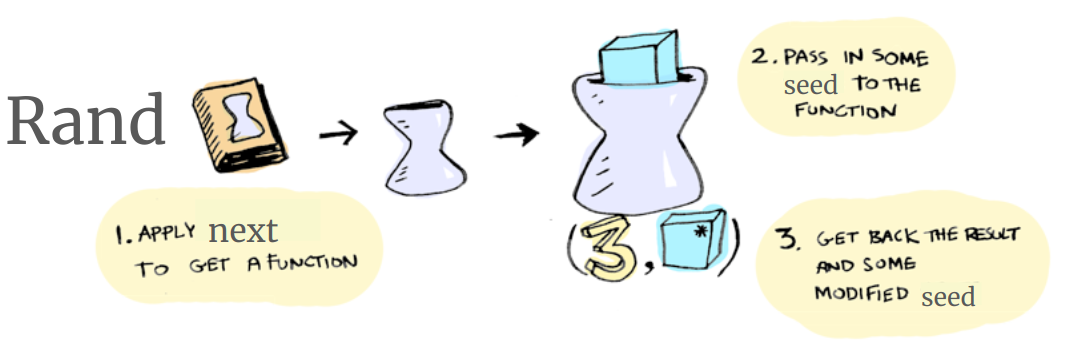
newtype Rand a = Rand { next :: Seed -> (Seed, a) }

Rand is a newtype wrapper around a function with type Seed -> (Seed, a). It represents a computation that, given a starting Seed, produces:

  1. A new updated Seed.
  2. A value of type a.

Here it is in pictures sloppily edited from adit.io’s excellent FunctorsA type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure. , ApplicativesA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). and MonadsA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. in Pictures. Rand Monad

Functor

Definition of Functor. The Functor instance for Rand allows you to map a function over the result of a random computation.

instance Functor Rand where
  fmap :: (a -> b) -> Rand a -> Rand b
  fmap f (Rand g) = Rand h
    where
      -- The function inside rand
      -- Apply f to the `value` a
      h seed = (newSeed, f a)
        where
          (newSeed, a) = g seed

fmap constructs a new Rand value, Rand h, by:

  1. Taking a function f and a random computation Rand g.
  2. Defining a new function h that, given an initial Seed, runs g to get (newSeed, a).
  3. Returning (newSeed, f a), where f a is the transformed value.

After applying fmap f, we have a new random computation that takes the same Seed as input and produces a transformed value (f a), while maintaining the same mechanics of randomness (i.e., correctly passing and updating the Seed state).

We can also be a bit more succinct, by making use of fmap instances

fmap :: (a -> b) -> Rand a -> Rand b
fmap f r = Rand $ (f <$>)<$> next r

Applicative

pure :: a -> Rand a
pure x = Rand (,x) -- Return the input seed and the value


(<*>) :: Rand (a -> b) -> Rand a -> Rand b
left <*> right = Rand h
where
    h s = (s'', f v) -- Need to return a function of type (Seed -> (Seed, Value))
    where
        (s', f) = next left s   -- Get the next seed and function from the left Rand
        (s'', v) = next right s' -- Get the next seed and value from the right Rand

<*> constructs a new Rand value Rand h by:

  1. Extracting a function f from the left computation using the initial seed.
  2. Using the new seed to extract a value v from the right computation.
  3. Returning a new seed and the result of applying f to v.
  4. This allows us to apply a random function to a random value in a sequence while maintaining proper state management of the Seed.

Monad

instance Monad Rand where
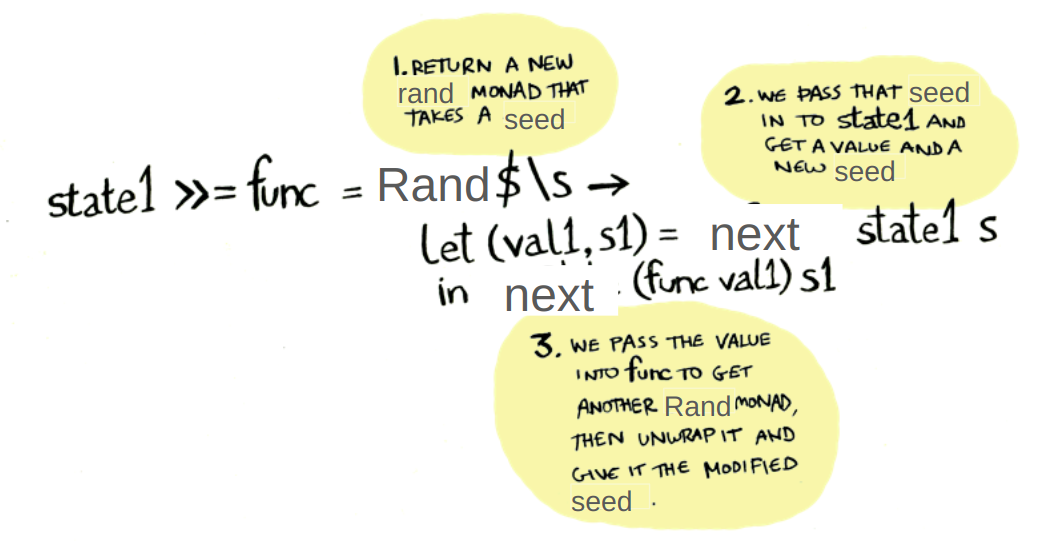
  (>>=) :: Rand a -> (a -> Rand b) -> Rand b
  r >>= f = Rand $ \s -> 
    let (s1, val) = next r s
    in next (f val) s1

r >>= f creates a new Rand computation by:

  1. Running the first computation r with the initial seed s.
  2. Extracting the value val and the new seed s1.
  3. Using val to determine the next random computation f val.
  4. Running f val with the updated seed s1 to produce the final result.

Bind

Get and Put

put is used to set the internal state (the Seed) of the Rand monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. . There is no value yet, hence we use the unitA type with exactly one value, (), used to indicate the absence of meaningful return value, similar to void in other languages. (())

put allows us to modify the internal state (Seed) of a random computation.

put :: Seed -> Rand ()
put newSeed = Rand $ \_ -> (newSeed, ())

get is used to retrieve the current state (the Seed) from the Rand monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. . It does not modify the state but instead returns the current seed as the result. This is achieved by putting the current seed in to the value part of the tuple.

Since, when we apply transformation on the tuple, we apply the transformation according to the value!

get :: Rand Seed
get = Rand $ \s -> (s, s)

Using get and the monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. instance, we can make a function to increase the seed by one.

incrementSeed' :: Rand Seed
incrementSeed' = get >>= \s -> pure (s + 1) 

incrementSeed :: Rand Seed
incrementSeed = do
  seed <- get  -- This gets the current seed
  return (seed + 1)  -- Increment the seed and put it in the 'state', we can do anything with the seed!

>>> next incrementSeed' 123
(123, 124)

Modifying a seed

We want to modify the seed, assuming there is no value. This will simply apply a function f to the current seed.

modify :: (Seed -> Seed) -> Rand ()
modify f = Rand $ \s -> (f s, ())

We can also write this using our get and put

modify :: (Seed -> Seed) -> Rand ()
modify f = get >>= \s -> put (f s)

This function:

  1. First retrieves the current seed (get).
  2. Applies the function f to modify the seed.
  3. Updates the internal state with put.

This computation returns () as its result, indicating that its purpose is to update the state, not to produce a value.

We can now write our incrementSeed in terms of modify

incrementSeed :: Rand Seed
incrementSeed = do
  modify (+1)   -- Use `modify` to increment the seed by 1
  get           -- Return the updated seed

Rolling A Dice

Let’s revisit the dice rolling example, but use the Rand monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. to thread the seed through all of our functions without us having to pass it around as a separate parameter. First recall our nextSeed and genRand functions:

nextSeed :: Seed -> Seed
nextSeed prevSeed = (a*prevSeed + c) `mod` m
  where -- Parameters for linear congruential RNG.
    a = 1664525
    c = 1013904223
    m = 2^32

-- | Generate a number between `l` and `u`.
genRand :: Int -> Int -> Seed -> Int
genRand l u seed = seed `mod` (u-l+1) + l

Using the above two functions and our knowledge, we can make a function which rolls a dice. This will require 3 parts.

  1. Using nextSeed to update the current seed
  2. Get the seed from the state
  3. Call genRand to get the integer.
rollDie :: Rand Int
rollDie = do
  modify nextSeed -- update the current seed
  s <- get -- get retrieves the updated seed value s from the Rand monad's state.
  pure (genRand 1 6 s) -- computes a random number and puts back in the context

We can also write this using bindthe defining function which all monads must implement. notation, where we modify nextSeed to update the seed. We then use >> to ignore the result (i.e., the ()). We use get to put the seed as the value, which is then binded on to s and used to generate a random number. We then use pure to update the value, the seed updating is handled by our bindthe defining function which all monads must implement. !

rollDie :: Rand Int
rollDie = modify nextSeed >> get >>= \s -> pure (genRand 1 6 s)

Finally, how we can use this?

>>> next rollDie 123
(1218640798,5)

next is used on rollDie to get the function of type Seed -> (Seed, a). We then call this function with a seed value of 123, to get a new seed and a dice roll.

Now, here’s how we get a list of dice rolls using a direct adaptation of our previous code, but trusting the Rand monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. to thread the Seed through for us. No more messy wiring up of parameters and inventing arbitrary variable names.

-- | Roll a six-sided die `n` times.
-- >>> runState (diceRolls 3) 123
-- ([5,4,1],166005888)
diceRolls :: Int -> Rand [Int]
diceRolls 0 = pure []
diceRolls n = do
  r <- rollDie
  rest <- diceRolls (n-1)
  pure (r:rest)

State Monad

Of course, Haskell libraries are extensive, and if you can think of useful code that’s generalisable, there’s probably a version of it already in the libraries somewhere.

Actually, we’ll use two libraries.

From System.Random, we’ll replace our Seed type with StdGen and nextSeed/genRand with randomR.

We’ll use Control.Monad.State to replace our Rand monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. . The State monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. provides a context in-which data can be threaded through function calls without additional parameters. Similar to our Rand monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. the data can be accessed with a get function, replaced with put, or updated with modify.

In diceRolls, we’ll also replace the recursive list construction, with replicateM, which just runs a function with a monadic effect n times, placing the results in a list.

module StateDie
where

import System.Random
import Control.Monad.State

-- | Here's a starting seed for our tests.
-- In System.Random seeds have type StdGen.
seed :: StdGen
seed = mkStdGen 123

-- | Remake the Rand monad, but using the State monad to store the seed
type Rand a = State StdGen a

-- | A function that simulates rolling a six-sided dice
-- >>> runState rollDie seed
-- (1,StdGen ...)
rollDie :: Rand Int
rollDie = state (randomR (1,6))

-- | Roll a six-sided die `n` times.
-- >>> runState (diceRolls 3) seed
-- ([1,5,6],StdGen ...)
diceRolls :: Int -> Rand [Int]
diceRolls n = replicateM n rollDie

As you can see, there is now very little custom code required for this functionality. Note that there is also a readonly version of the State monadA type class in Haskell that represents computations as a series of steps. It provides the bind operation (»=) to chain operations and the return (or pure) function to inject values into the monadic context. , called Reader, as well as a write-only version (e.g. for tasks like logging) called Writer.