In this chapter we will meet some more typeclasses that abstract common coding patterns for dealing with data.

Learning Outcomes

Folds

Recall the “reduce” function that is a member of JavaScript’s Array type, and which we implemented ourselves for linked and cons lists, was a way to generalise loops over enumerable types. In Haskell, this concept is once again generalised with a typeclass called Foldable – the class of things which can be “folded” over to produce a single value.
We will come back to the Foldable typeclass, but first let’s limit our conversation to the familiar Foldable instance, basic lists.
Although in JavaScript reduce always associates elements from left to right, Haskell’s Foldable typeclass offers both foldl (which folds left-to-right) and foldr (which folds right-to-left):

Prelude> :t foldl
foldl :: Foldable t => (b -> a -> b) -> b -> t a -> b

Prelude> :t foldr
foldr :: Foldable t => (a -> b -> b) -> b -> t a -> b

In the following examples, the Foldable t instance is a list. Here’s how we right-fold over a list to sum its elements:

Left Fold

While the lambda above makes it explicit which parameter is the accumulator and which is the list element, this is a classic example where point-free coding style makes this expression very succinct:

Prelude> foldr (+) 0 [5,8,3,1,7,6,2]

32

Here’s a left fold with a picture of the fold:

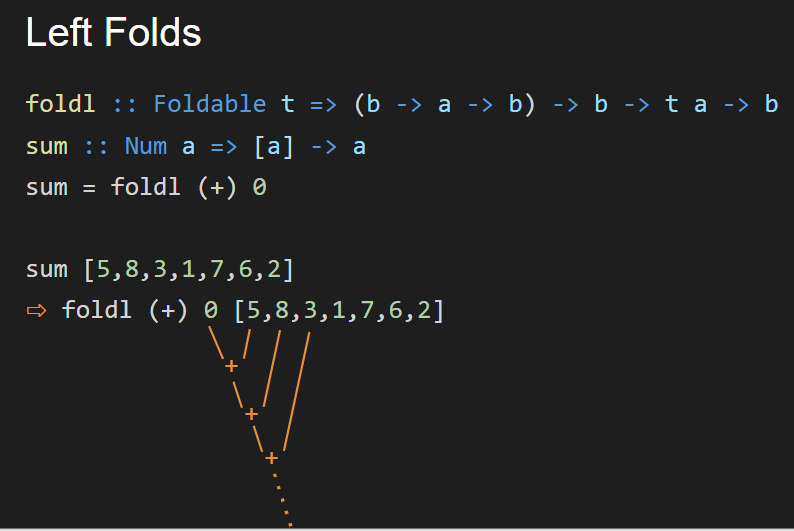
Left Fold

Note that since the (+) operator is associative—a+(b+c) = (a+b)+c—foldr and foldl return the same result. For functions that are not associative, however, this is not necessarily the case.

Exercises

  1. Predict what the results of a left- and right-fold will be for (-) folded over [1,2,3,4] with initial value 0.
  2. What is the result of foldr (:) [] applied to any list?
  3. Implement map using foldr.

Solutions

  1. The right fold processes the list from the right (end) to the left (beginning). The result of each application of the function is passed as the accumulator to the next application.
    foldr (-) 0 [1,2,3,4]
   = 1 - (2 - (3 - (4 - 0)))
   = 1 - (2 - (3 - 4))
   = 1 - (2 - (-1))
   = 1 - 3
   = -2

The left fold processes the list from the left (beginning) to the right (end). The result of each application of the function is passed as the accumulator to the next application.

   foldl (-) 0 [1,2,3,4]
   = (((0 - 1) - 2) - 3) - 4
   = ((-1 - 2) - 3) - 4
   = (-3 - 3) - 4
   = -6 - 4
   = -10
  1. The function foldr (:) [] applied to any list essentially reconstructs the list
  foldr (:) [] [1, 2, 3, 4]
   = 1 : (2 : (3 : (4 : [])))
  1. Taking intuition from the previous question, we know that (:) does not change the list, but reconstructs it. Therefore, to implement map, we just apply the function f to the list as we go.
  map :: (a -> b) -> [a] -> [b]
  map f = foldr (\x acc -> f x : acc) []

Or, by making the lambda function point-free

  map :: (a -> b) -> [a] -> [b]
  map f = foldr ((:) . f) []

Monoid

In the example fold above, we provide the (+) function to tell foldl how to aggregate elements of the list. There is also a typeclass for things that are “automatically aggregable” or “concatenatable” called Monoid which declares a general function for mappend combining two Monoids into one, a mempty value such that any MonoidA type class for types that have an associative binary operation (mappend) and an identity element (mempty). Instances of Monoid can be concatenated using mconcat. mappend‘ed with mempty is itself, and a concatenation function for lists of Monoid called mconcat.

Prelude> :i Monoid
class Semigroup a => Monoid a where
  mempty :: a
  mappend :: a -> a -> a
  mconcat :: [a] -> a
  {-# MINIMAL mempty #-}
...

In the Data.Monoid library, there are some interesting instances of MonoidA type class for types that have an associative binary operation (mappend) and an identity element (mempty). Instances of Monoid can be concatenated using mconcat. . For example, Sum is an instance of MonoidA type class for types that have an associative binary operation (mappend) and an identity element (mempty). Instances of Monoid can be concatenated using mconcat. which wraps a Num, such that lists of Sum can be mconcated:

Prelude> import Data.Monoid
Data.Monoid> mconcat $ Sum <$> [5,8,3,1,7,6,2]

Sum {getSum = 32}

So a sum is a data type with an accessor function getSum that we can use to get back the value:

Prelude Data.Monoid> getSum $ mconcat $ Sum <$> [5,8,3,1,7,6,2]

32

We make a data type aggregable by instancing Monoid and providing definitions for the functions mappend and mempty. For Sum these will be (+) and 0 respectively. Lists are also themselves Monoidal, with mappend defined as an alias for list concatenation (++), and mempty as []. Thus, we can:

Prelude Data.Monoid> mconcat [[1,2],[3,4],[5,6]]
[1,2,3,4,5,6]

which has a simple alias concat defined in the PreludeThe default library loaded in Haskell that includes basic functions and operators. :

Prelude> concat [[1,2],[3,4],[5,6]]
[1,2,3,4,5,6]

There is also an operator for mappend called (<>), such that the following are equivalent:

Data.Monoid> mappend (Sum 1) (Sum 2)
Sum {getSum = 3}

Data.Monoid> (Sum 1) <> (Sum 2)
Sum {getSum = 3}

And for lists (and String) we have:

> mappend [1,2] [3,4]
[1,2,3,4]

> [1,2] <> [3,4]
[1,2,3,4]

> [1,2] ++ [3,4]
[1,2,3,4]

Foldable

So now we’ve already been introduced to foldl and foldr for lists, and we’ve also seen the Monoid typeclass. Let’s take a look at the general class of things that are Foldable. As always, your best friend for exploring a new typeclass in Haskell is GHCi’s :i command:

Prelude> :i Foldable
class Foldable (t :: * -> *) where
  foldr :: (a -> b -> b) -> b -> t a -> b -- as described previously, but notice foldr and foldl
  foldl :: (b -> a -> b) -> b -> t a -> b -- are for any Foldable t, not only lists
  length :: t a -> Int -- number of items stored in the Foldable
  null :: t a -> Bool -- True if empty
  elem :: Eq a => a -> t a -> Bool -- True if the a is an element of the t of a
  maximum :: Ord a => t a -> a -- biggest element in the Foldable
  minimum :: Ord a => t a -> a -- smallest element
  sum :: Num a => t a -> a -- compute the sum of a Foldable of Num
  product :: Num a => t a -> a -- compute the product of a Foldable of Num
  Data.Foldable.fold :: Monoid m => t m -> m -- if the elements of t are Monoids then we don’t need an operator to aggregate them
  foldMap :: Monoid m => (a -> m) -> t a -> m -- uses the specified function to convert elements to Monoid and then folds them
  Data.Foldable.toList :: t a -> [a] -- convert any Foldable things to a list
  {-# MINIMAL foldMap | foldr #-}
        -- Defined in `Data.Foldable'
instance Foldable [] -- Defined in `Data.Foldable'
instance Foldable Maybe -- Defined in `Data.Foldable'
instance Foldable (Either a) -- Defined in `Data.Foldable'
instance Foldable ((,) a) -- Defined in `Data.Foldable'

Note that I’ve reordered the list of functions to the order we want to discuss them, removed a few things we’re not interested in at the moment and the comments are mine. However, once you get used to reading types, the :info for this class is pretty self-explanatory. Most of these functions are also familiar from their use with lists. The surprise (OK, not really) is that lots of other things can be Foldable as well.

Prelude> foldr (-) 1 (Just 3)
2
Prelude> foldl (-) 1 (Just 3)
-2
Prelude> foldr (+) 1 (Nothing)
1
Prelude> length (Just 3)
1
Prelude> length Nothing
0
-- etc

If we import the Data.FoldableA type class for data structures that can be folded (reduced) to a single value. It includes functions like foldr, foldl, length, null, elem, maximum, minimum, sum, product, and foldMap. namespace we also get fold and foldMap, which we can use with Monoid types which know how to aggregate themselves (with mappend):

Prelude> import Data.Foldable

Prelude Data.Foldable> fold [[1,2],[3,4]] -- since lists are also Monoids
[1,2,3,4]

The fun really starts though now that we can make new Foldable things:

data Tree a = Empty
            | Leaf a
            | Node (Tree a) a (Tree a)
  deriving (Show)

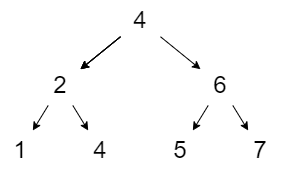
tree = Node (Node (Leaf 1) 2 (Leaf 3)) 4 (Node (Leaf 5) 6 (Leaf 7))

Which produces a tree with this structure:

Tree

We make this type of binary tree an instance of foldableA type class for data structures that can be folded (reduced) to a single value. It includes functions like foldr, foldl, length, null, elem, maximum, minimum, sum, product, and foldMap. by implementing either of the minimum defining functions, foldMap or foldr:

instance Foldable Tree where
  foldMap :: Monoid m => (a -> m) -> Tree a -> m
  foldMap _ Empty = mempty
  foldMap f (Leaf x) = f x
  foldMap f (Node l x r) = foldMap f l <> f x <> foldMap f r

> length tree
7
> foldr (:) [] tree
[1,2,3,4,5,6,7]

We can use foldMap to map the values stored in the tree to an instance of Monoid and then concatenate these Monoids. For example, we could map and concatenate them as a Sum:

> getSum $ foldMap Sum tree
28

Or we can compute the same conversion to a list as the above foldr, by providing foldMap with a function that places the values into singleton lists, e.g.:

> (:[]) 1 -- cons 1 with an empty list, same as 1:[]
[1]

Since list is an instance of MonoidA type class for types that have an associative binary operation (mappend) and an identity element (mempty). Instances of Monoid can be concatenated using mconcat. , foldMap will concatenate these singleton lists together:

> foldMap (:[]) tree
[1,2,3,4,5,6,7]

Exercise

  • Make an instance of Foldable for Tree in terms of foldr instead of foldMap.

Solutions

instance Foldable Tree where
  foldr :: (a -> b -> b) -> b -> Tree a -> b
  foldr _ z Empty = z -- base case, return accumulator
  foldr f z (Leaf x) = f x z -- when we see a leaf, combine accumulator and leaf
  foldr f z (Node l x r) = foldr f (f x (foldr f z r)) l -- fold over right first, then over left

Traversable

Traversable extends both Foldable and Functor, in a typeclass for things that we can traverse a function with an Applicative effect over. Here’s a sneak peek of what this lets us do:

Prelude> traverse putStrLn ["tim","was","here"]
tim
was
here
[(),(),()]

The first three lines are the strings printed to the terminal (the side effect). The result reported by GHCi is a list [(),(),()] as discussed below.

Here, as usual, is what GHCi :i tells us about the TraversableA type class for data structures that can be traversed, applying a function with an Applicative effect to each element. It extends both Foldable and Functor and includes functions like traverse and sequenceA. type classA type system construct in Haskell that defines a set of functions that can be applied to different types, allowing for polymorphic functions. :

Prelude> :i Traversable
class (Functor t, Foldable t) => Traversable (t :: * -> *) where
  traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
  sequenceA :: Applicative f => t (f a) -> f (t a)
  ... -- some other functions
  {-# MINIMAL traverse | sequenceA #-}
        -- Defined in `Data.Traversable'
instance Traversable [] -- Defined in `Data.Traversable'
instance Traversable Maybe -- Defined in `Data.Traversable'
instance Traversable (Either a) -- Defined in `Data.Traversable'
instance Traversable ((,) a) -- Defined in `Data.Traversable'

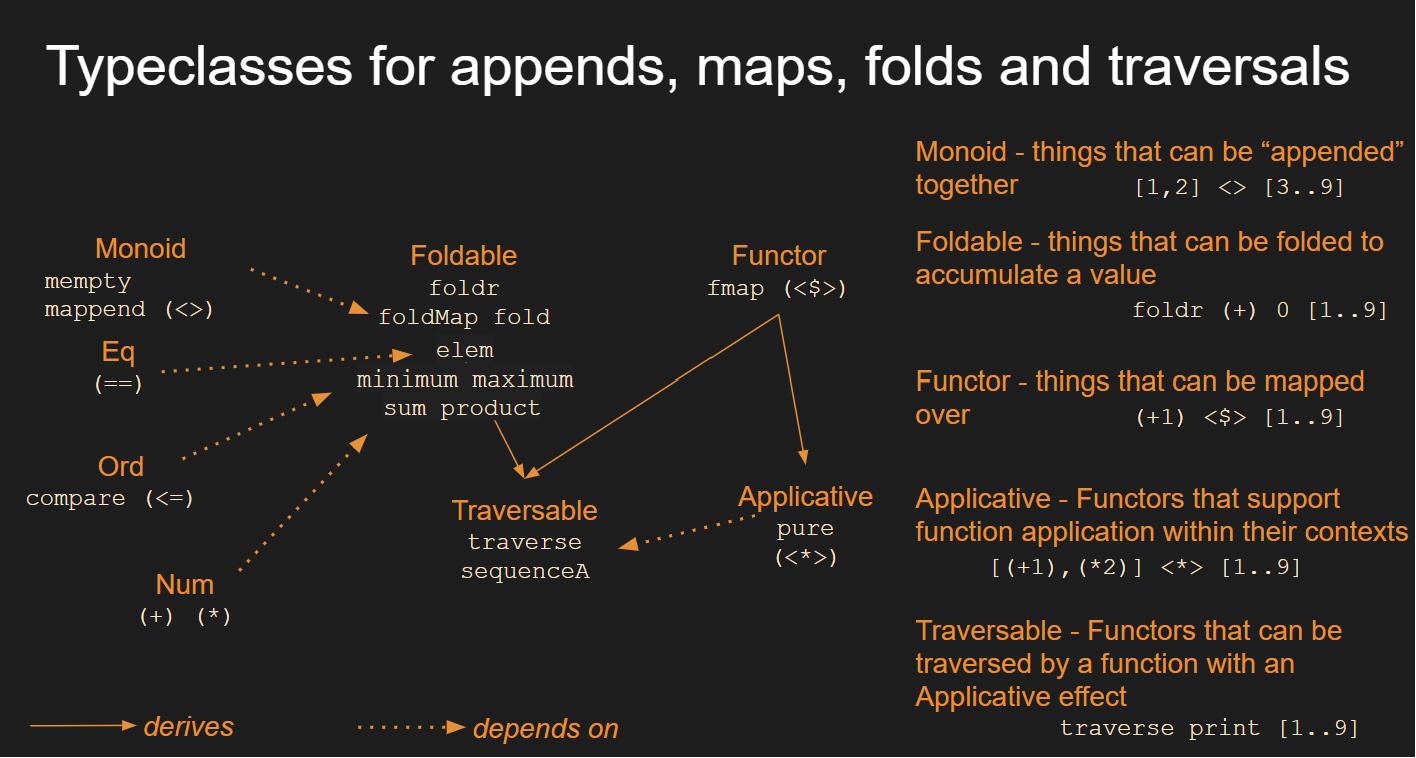
The following map shows how all of these typeclasses are starting to come together to offer some real power:

Traversable Typeclasses

So what does the traverse function do? By way of example, remember our safe modulo function we used to experiment with FunctorA type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure. :

safeMod :: Integral a => a-> a-> Maybe a
safeMod _ 0 = Nothing
safeMod numerator divisor = Just $ mod numerator divisor

It lets us map over a list of numbers without throwing divide-by-zero exceptions:

> map (safeMod 3) [1,2,0,2]
[Just 0,Just 1,Nothing,Just 1]

But what if 0s in the list really are indicative of disaster such that we should bail rather than proceeding? The traverse function of the Traversable type-class gives us this kind of “all or nothing” capability:

> traverse (safeMod 3) [1,2,0,2]
Nothing
> traverse (safeMod 3) [1,2,2]
Just [0,1,1]

So mapping a function with an Applicative effect over the values in a list gives us back a list with each of those values wrapped in the effect. However, traverseing such a function over a list gives us back the list of unwrapped values, with the whole list wrapped in the effect.

Traverse applies a function with a result in an Applicative context (i.e. an ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). effect) to the contents of a Traversable thing.

Prelude> :t traverse
traverse
  :: (Applicative f, Traversable t) => (a -> f b) -> t a -> f (t b)

What are some other functions with ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). effects? Lots! E.g.:

  • Any constructor of a data type that instances ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). : e.g. Just :: a -> Maybe a
  • Anything that creates a list: (take 5 $ repeat 1) :: Num a => [a]
  • IO is ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). , so a function like print :: Show a => a -> IO ()
  • etc…

The print function converts values to strings (using show if available from an instance of Show) and sends them to standard-out. The print function wraps this effect (there is an effect on the state of the console) in an IO computational context:

Prelude> :t print
print :: Show a => a -> IO ()

The () is like void in TypeScript—it’s a type with exactly one value (), and hence is called “UnitA type with exactly one value, (), used to indicate the absence of meaningful return value, similar to void in other languages. ”. There is no return value from print, only the IO effect, and hence the return type is (). IO is also an instance of Applicative. This means we can use traverse to print out the contents of a list:

Prelude> traverse print [1,2,3]
1
2
3
[(),(),()]

Here 1,2,3 are printed to the console each on their own line (which is print’s IO effect), and [(),(),()] is the return value reported by GHCi—a list of UnitA type with exactly one value, (), used to indicate the absence of meaningful return value, similar to void in other languages. .

Prelude> :t traverse print [1,2,3]
traverse print [1,2,3] :: IO [()]

When we ran this at the REPL, GHCi consumed the IO effect (because it runs all commands inside the IO Monad). However, inside a pure functionA function that always produces the same output for the same input and has no side effects. there is no easy way to get rid of this IO return type—which protects you from creating IO effects unintentionally.

A related function defined in Traversable is sequenceA which allows us to convert directly from TraversablesA type class for data structures that can be traversed, applying a function with an Applicative effect to each element. It extends both Foldable and Functor and includes functions like traverse and sequenceA. of ApplicativesA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). , to ApplicativesA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). of TraversablesA type class for data structures that can be traversed, applying a function with an Applicative effect to each element. It extends both Foldable and Functor and includes functions like traverse and sequenceA. :

> :t sequenceA
sequenceA :: (Applicative f, Traversable t) => t (f a) -> f (t a)
Prelude> sequenceA [Just 0,Just 1,Just 1]
Just [0,1,1]
Prelude> sequenceA [Just 0,Just 1,Nothing,Just 1]
Nothing

The default sequenceA is defined very simply in terms of traverse (recall id is just \x->x):

sequenceA = traverse id

A bit more fun with sequenceA, a list of functions:

> :t [(+3),(*2),(+6)]
[(+3),(*2),(+6)] :: Num a => [a -> a]

is also a list of Applicative, because function (->)r is an instance of Applicative. Therefore, we can apply sequenceA to a list of functions to make a single function that applies every function in the list to a given value and return a list of the results:

> :t sequenceA [(+3),(*2),(+6)]
sequenceA [(+3),(*2),(+6)] :: Num a => a -> [a]
> sequenceA [(+3),(*2),(+6)] 2
[5,4,8]

To create our own instance of Traversable we need to implement fmap to make it a Functor and then either foldMap or foldr to make it Foldable and finally, either traverse or sequenceA. So for our Tree type above, which we already made Foldable we add:

instance Functor Tree where
   fmap :: (a -> b) -> Tree a -> Tree b
   fmap _ Empty = Empty
   fmap f (Leaf x) = Leaf $ f x
   fmap f (Node l v r) = Node (fmap f l) (f v) (fmap f r)

instance Traversable Tree where
   traverse :: Applicative f => (a -> f b) -> Tree a -> f (Tree b)
   traverse _ Empty = pure Empty
   traverse f (Leaf a) = Leaf <$> f a
   traverse f (Node l x r) = Node <$> traverse f l <*> f x <*> traverse f r

So now we can traverse a function with an Applicative effect over the tree:

Prelude> traverse print tree
1
2
3
4
5
6
7

And of course, we can sequence a Tree of Maybes into a Maybe Tree:

> treeOfMaybes = Just <$> tree -- a tree of Maybes
> treeOfMaybes
Node (Node (Leaf (Just 1)) (Just 2) (Leaf (Just 3))) (Just 4) (Node (Leaf (Just 5)) (Just 6) (Leaf (Just 7)))
> sequenceA treeOfMaybes
Just (Node (Node (Leaf 1) 2 (Leaf 3)) 4 (Node (Leaf 5) 6 (Leaf 7)))

Applying Functions Over Contexts

Thus far we have seen a variety of functions for applying functions in and over different contexts. It is useful to note the similarities between these, and recognise that they are all doing conceptually the same thing, i.e. function application. The difference is in the type of context. The simplest function for applying functions is the ($) operator, with just a function (no context), applied directly to a value. Then fmap, just a function, mapped over a FunctorA type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure. context/container. Then ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). (function also in the context). Then, most recently traverse: the function produces a result in an ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). context, applied (traversed) over some data structure, and the resulting data structure returned in an ApplicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). context. Below, I line up all the types so that the similarities and differences are as clear as possible. It’s worth making sure at this stage that you can read such type signatures, as they really do summarise everything that we have discussed.

($)      ::                                      (a -> b) -> a   -> b
(<$>)    :: Functor f                      =>    (a -> b) -> f a -> f b
(<*>)    :: Applicative f                  =>  f (a -> b) -> f a -> f b
traverse :: (Traversable t, Applicative f) =>  (a -> f b) -> t a -> f (t b)

Parsing a String Using Traversable?

What if we want to parse an exact match for a given string, for example, a token in a programming language like the word function. Or, to look for a polite greeting at the start of an email before deciding whether to respond, such as “hello”.

> parse (string "hello") "hello world"
Just (" world", "hello")

> parse (string "hello") "world, hello"
Nothing

So the string “hello” is the prototype for the expected input. How would we do this?

Our parserA function or program that interprets structured input, often used to convert strings into data structures. would have to process characters from the input stream and check if each successive character is the one expected from the prototype. If it is the correct character, we would cons it to our result and then parse the next character.

This can have a recursive solution:

string [] = pure ""
string (x:xs) = liftA2 (:) (is x) (string xs)

We parse the first character, x, then recursively parse the rest of the string. We lift the (:) operator into the parserA function or program that interprets structured input, often used to convert strings into data structures. context to combine our results into a single list. This can also be written using a foldr to parse all the characters while checking with the is parserA function or program that interprets structured input, often used to convert strings into data structures. .

string l = foldr (\c acc -> liftA2 (:) (is c) acc) (pure "") l

Remembering liftA2 is equivalent to f <$> a <*> b.

Our <*> will allow for the sequencing of the applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). effect, so this will sequentially parse all characters, making sure they are correct. As soon as one applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). parserA function or program that interprets structured input, often used to convert strings into data structures. fails, the result of the parsing will fail.

This could also be written as:

string l = foldr cons (pure []) l
  where
    cons c acc = liftA2 (:) (is c) acc

But the title of this section was traverse?

Well, let’s consider how we would define a list as an instance of the traversableA type class for data structures that can be traversed, applying a function with an Applicative effect to each element. It extends both Foldable and Functor and includes functions like traverse and sequenceA. operator. The traverse function is defined for lists exactly as follows:

instance Traversable [] where
  traverse :: Applicative f => (a -> f b) -> [a] -> f [b]
  traverse f = foldr cons (pure [])
    where cons x ys = liftA2 (:) (f x) ys

This is almost exactly the definition of our string parserA function or program that interprets structured input, often used to convert strings into data structures. using foldr but the function f is exactly the is ParserA function or program that interprets structured input, often used to convert strings into data structures. .

Therefore, we can write string = traverse is

Let’s break down how the string parserA function or program that interprets structured input, often used to convert strings into data structures. using traverse and is works in terms of types:

string :: String -> Parser String
string = traverse is

traverse is a higher-order functionA function that takes other functions as arguments or returns a function as its result. with the following type:

traverse :: (Traversable t, Applicative f) => (a -> f b) -> t a -> f (t b)

t is a traversableA type class for data structures that can be traversed, applying a function with an Applicative effect to each element. It extends both Foldable and Functor and includes functions like traverse and sequenceA. data structure, which in our case is a String (since String is a list of characters). a is the element type of the traversableA type class for data structures that can be traversed, applying a function with an Applicative effect to each element. It extends both Foldable and Functor and includes functions like traverse and sequenceA. structure, which is Char (the individual characters in the String). f is an applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). functorA type class in Haskell that represents types that can be mapped over. Instances of Functor must define the fmap function, which applies a function to every element in a structure. , which is the Parser type in our case. The function (a -> f b) is the parserA function or program that interprets structured input, often used to convert strings into data structures. for a single character. In our case, it’s the is parserA function or program that interprets structured input, often used to convert strings into data structures. .

So, we will apply the is function to each element in the traversableA type class for data structures that can be traversed, applying a function with an Applicative effect to each element. It extends both Foldable and Functor and includes functions like traverse and sequenceA. t (the list) and collect the result into a Parser [Char].

Therefore, traverse is is of type Parser String, which is a parserA function or program that interprets structured input, often used to convert strings into data structures. that attempts to parse the entire String and returns it as a result.

Can we also write this using sequenceA?

string :: String -> Parser String
string str = sequenceA (map is str)

Or in point-free form

string :: String -> Parser String
string = sequenceA . map is

map is str maps the is parserA function or program that interprets structured input, often used to convert strings into data structures. over each character in the input string str. This produces a list of parsersA function or program that interprets structured input, often used to convert strings into data structures. , where each parserA function or program that interprets structured input, often used to convert strings into data structures. checks if the corresponding character in the input matches the character in the target string.

sequenceA is then used to turn the list of parsersA function or program that interprets structured input, often used to convert strings into data structures. into a single parserA function or program that interprets structured input, often used to convert strings into data structures. . This function applies each parserA function or program that interprets structured input, often used to convert strings into data structures. to the input string and collects the results. If all character parsersA function or program that interprets structured input, often used to convert strings into data structures. succeed, it returns a list of characters; otherwise, it returns Nothing.

In fact an equivalent definition of traverse can be written using the sequenceA as follows:

traverse :: (Traversable t, Applicative f) => (a -> f b) -> t a -> f (t b)
traverse f l = sequenceA (f <$> l)

Exercises

  • What would be the definition of sequenceA over a list? (without using traverse)
  • Can you make the Maybe data type an instance of traversableA type class for data structures that can be traversed, applying a function with an Applicative effect to each element. It extends both Foldable and Functor and includes functions like traverse and sequenceA. ?

Solutions

  • sequenceA takes a list of applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). actions and returns an applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). action that returns a list of results. For lists, this means that sequenceA should combine a list of applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). actions into a single applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). action that returns a list of results.

    sequenceA :: (Applicative f) => [f a] -> f [a]
sequenceA [] = pure []
sequenceA (x:xs) = (:) <$> x <*> sequenceA xs

  • For Maybe, the definition of traverse function is traverse :: (Applicative f) => (a -> f b) -> Maybe a -> f (Maybe b)

    instance Traversable Maybe where
  traverse :: (Applicative f) => (a -> f b) -> Maybe a -> f (Maybe b)
  traverse _ Nothing = pure Nothing
  traverse f (Just x) = Just <$> f x
    • If the input is Nothing, we return pure Nothing, which is an applicativeA type class in Haskell that extends Functor, allowing functions that are within a context to be applied to values that are also within a context. Applicative defines the functions pure and (<*>). action that produces Nothing.
    • If the input is Just x, we apply f to x and then wrap the result with Just.

Bringing it all together

We can also parse a tree by traversing a parserA function or program that interprets structured input, often used to convert strings into data structures. over it, the same way we parsed string by traversing a list of Char!

Recall from earlier in this section:

data Tree a = Empty
            | Leaf a
            | Node (Tree a) a (Tree a)
  deriving (Show)

instance Traversable Tree where
  --  traverse :: Applicative f => (a -> f b) -> Tree a -> f (Tree b)
  traverse _ Empty = pure Empty
  traverse f (Leaf a) = Leaf <$> f a
  traverse f (Node l x r) = Node <$> traverse f l <*> f x <*> traverse f r

We can write a similar definition for parsing an exact tree compared to parsing a string!

We will consider a Value which is either an integer, or an operator which can combine integers. We will assume the only possible combination operator is + to avoid complexities with ordering expressions.

data Value = Value Int | BinaryPlus
  deriving (Show)

We can generalise the is parserA function or program that interprets structured input, often used to convert strings into data structures. to satisfy, which will run a given parserA function or program that interprets structured input, often used to convert strings into data structures. p, and make sure the result satisfies a boolean condition.

satisfy :: Parser a -> (a -> Bool) -> Parser a
satisfy p f = Parser $ \i -> case parse p i of
  Just (r, v)
      | f v -> Just (r, v)
  _ -> Nothing

From this satisfy, we will use traverse to ensure our string exactly matches a wanted expression Tree.

isValue :: Value -> Parser Value
isValue (Value v) = Value <$> satisfy int (==v)
isValue BinaryPlus = BinaryPlus <$ satisfy char (=='+')

stringTree :: Tree Value -> Parser (Tree Value)
stringTree = traverse isValue

sampleTree :: Tree Value
sampleTree =
  Node
    (Leaf $ Value 3)
    BinaryPlus
    (Node
      (Leaf (Value 5))
      BinaryPlus
      (Leaf (Value 2)))


inputString :: String
inputString = "3+5+2"

parsedResult :: String -> Maybe (String, Tree Value)
parsedResult = parse (stringTree sampleTree) inputString

The parsedResult will only succeed if the input string exactly matches the desired tree.

>>> parsedResult
Just ("",Node (Leaf (Value 3)) BinaryPlus (Node (Leaf (Value 5)) BinaryPlus (Leaf (Value 2))))

To evaluate the parsed expression we can use foldMap and the Sum monoidA type class for types that have an associative binary operation (mappend) and an identity element (mempty). Instances of Monoid can be concatenated using mconcat. :

evalTree :: Tree Value -> Int
evalTree tree = getSum $ foldMap toSum tree
  where
    toSum :: Value -> Sum Int
    toSum (Value v) = Sum v
    toSum BinaryPlus = Sum 0 -- For BinaryPlus, we don’t need to add anything to the sum

evalResult :: Maybe (String, Int)
evalResult = (evalTree <$>) <$> parsedResult
-- >>> evalResult = Just ("", 10)

Glossary

Folding: The process of reducing a data structure to a single value by applying a function. Haskell provides two types of folds: foldl (left fold) and foldr (right fold).

foldl: A left fold function that processes elements from left to right. Its type signature is foldl :: Foldable t => (b -> a -> b) -> b -> t a -> b.

foldr: A right fold function that processes elements from right to left. Its type signature is foldr :: Foldable t => (a -> b -> b) -> b -> t a -> b.

Monoid: A type class for types that have an associative binary operation (mappend) and an identity element (mempty). Instances of Monoid can be concatenated using mconcat.

Foldable: A type class for data structures that can be folded (reduced) to a single value. It includes functions like foldr, foldl, length, null, elem, maximum, minimum, sum, product, and foldMap.

Traversable: A type class for data structures that can be traversed, applying a function with an Applicative effect to each element. It extends both Foldable and Functor and includes functions like traverse and sequenceA.

Unit: A type with exactly one value, (), used to indicate the absence of a meaningful return value, similar to void in other languages.